Ответ
Задание 1. Известно, что сумма квадратов корней трёхчлена x2+3ax+3b равна сумме квадратов корней трёхчлена x2+3bx+3a. Чему равно a+b, если a≠b?
Задание 2. Известно, что F(F(x))=9x−4F. Какой может быть функция F(x)?
F(x)=9×2−4
F(x)=3√x−2
F(x)=3x+1
F(x)=3x−2
F(x)=3x−1
F(x)=(9x−4)2
Задание 3. Назовём простое число разложимым, если его можно представить в виде суммы 9 составных чисел (не обязательно различных). Найдите наибольшее простое число, которое не является разложимым.
Задание 4. Бумажный прямоугольник ABCD со сторонами AB=10 и BC=24 согнули по прямой так, что вершина D попала в вершину B. Найдите длину линии сгиба.
Задание 5. Ровно в полдень муравей выбегает из муравейника и по прямой тропинке бежит к полю. Через минуту вслед за ним выбегает второй муравей и бежит вслед за первым, но со скоростью на 1 см/мин большей, чем скорость первого. И так далее: каждую минуту из муравейника выбегает следующий муравей и бежит вдогонку за остальными со скоростью на 1 см/мин большей, чем скорость предыдущего. Какой по счёту муравей будет возглавлять процессию через 2 часа, если скорость первого муравья равна 70 см/мин? Если муравьёв будет несколько, укажите их всех.
Задание 6. На плоскости проведено 11 прямых. Известно, что если выбрать из этих прямых любые 4, то среди выбранных прямых найдутся хотя бы две параллельные. Какое наибольшее количество точек пересечения могут иметь между собой все проведённые прямые?
Задание 7. Коля придумал функцию f(x)=(x−100)(2x−200)(4x−400)−(ax3+bx2+cx+d)
При некоторых фиксированных значениях параметров (a, b, c, d) функция f(x) такова, что:
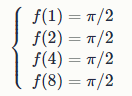
Найдите значение параметра aa.
Задание 8. Известно, что количество способов вырезать по линиям сетки из клетчатого квадрата N×N квадрат 2×2 в 6 раз меньше, чем количество способов вырезать из этого же квадрата фигуру Г-тетрамино (см. рисунок).
Найдите сторону N такого квадрата. Фигуру можно поворачивать и переворачивать.
