Ответ
Задание 1. Блины
На столе лежит стопка блинов. Между соседними блинами находится либо сметана, либо одна из двух сладких начинок мёд или варенье. Верхняя и нижняя стороны стопки блинов не покрыты никакими начинками.
Известно, что у каждого блина ровно одна сторона намазана сметаной. Кроме того, одна сторона у трети всех блинов покрыта вареньем, а у 10 блинов одна сторона покрыта мёдом. Найдите общее количество блинов в стопке.
Ответ 60 блинов
Задание 2. Выражение
Недавно Катя узнала про одну интересную операцию взятие остатка от деления. Обозначается она mod. К примеру, 13 mod5=3, так как при делении числа 13 на 5 получится целое число 2 и остаток 3: 13=5 ∗ 2+3. Таким образом, 26 mod9=8, а 21 mod3=0.
Катя очень любознательна, поэтому она решила изобрести новую операцию и составить задачу с её использованием. И вот что у девочки получилось.
Есть шесть карточек, на которых записаны числа 1, 2, 3, 4, 5, 6, и пять карточек с символом X. Данный символ обозначает некоторую операцию, которая определяется следующим образом: aXb=ab−a mod b, где mod операция взятия остатка от деления a на b. Например, 10X7=10⋅7−10 mod7=70−3=63. Здесь 3 это результат операции взятия остатка от деления 10 на 7.
Составьте из этих карточек правильное математическое выражение, значение которого было бы как можно большим. В ответ запишите строку, содержащую по одной цифре 1, 2, 3, 4, 5, 6 и пять символов X между данными цифрами. Необходимо использовать все карточки, выражение должно начинаться и заканчиваться цифрой.
Пример правильного выражения: 1X2X3X4X5X6. Вычисление данного выражения идёт слева направо, т.е. сначала посчитается значение 1X2, потом выражение (1X2)X3 и т.д. Например, 3X2X4 будет вычисляться следующим образом: сначала посчитаем 3X2=3⋅2−3 mod2=6−1=5, затем полученный результат будет участвовать в операции с 4:5X4=5⋅4−5 mod4=20−1=19. Чем больше окажется результат вашего выражения, тем больше баллов вы получите.
Ответ: 6Х1Х2Х3Х4Х5
Задание 3. Вёдра с водой
У Кати есть два пустых ведра A и B, имеющих различную ёмкость. Катя может проделывать следующие операции:
1. Набрать полное ведро A.
2. Набрать полное ведро B.
3. Перелить воду из ведра A в B до наполнения B (в ведре A может остаться вода) или до тех пор, пока A не опустеет.
4. Перелить воду из ведра B в A до наполнения A (в ведре B может остаться вода) или до тех пор, пока B не опустеет.
5. Опустошить ведро A.
6. Опустошить ведро B.
Ответьте на вопросы.
1. Известно, что ёмкость ведра A составляет 8 литров, а ведра B 6 литров. Найдите минимальную последовательность операций, которые необходимо выполнить Кате, чтобы после их выполнения в двух ведрах вместе было 4 литра воды. В ответ запишите номера операций без пробелов и запятых, например, 1316. В этом случае Катя сначала набирает воду в ведро A (операция 1), затем переливает из ведра A в ведро B воду (операция 3), потом снова набирает ведро A (операция 1) и, наконец, выливает воду из ведра B (операция 6).
2. Известно, что ёмкость ведра A составляет 8 литров, а ведра B 6 литров. Сколько различных ненулевых объёмов воды в двух вёдрах вместе можно получить в этом случае?
3. Известно, что ёмкость ведра A составляет 8 литров, а ведра B 5 литров. Запишите через пробел все возможные ненулевые объёмы воды, которые можно набрать в оба ведра вместе, используя не более 8 действий.
Ответ:
1) 2 4 2 4 5
2) 7
3) 2 3 5 6 7 8 10 11 13
Задание 4. Правда или ложь
Рядом с Кудыкиной горой есть три села: Правдино, Лжецово и Хитрецово. Достоверно известно, что в селе Правдино живут только правдолюбы, в селе Лжецово лжецы, а в селе Хитрецово хитрецы, которые не хотят, чтобы их обложили налогами, поэтому всегда лгут о своём местоположении, а обо всём остальном могут говорить и правду, и ложь.
Переписчик Иванов пошёл на хитрость: он опросил всех жителей, задавая каждому лишь три вопроса:
1. Ты из села Правдино?
2. Ты из села Лжецово?
3. Ты из села Хитрецово?
На первый вопрос он получил 360 ответов «Да», на второй вопрос и третий вопросы вместе 480 ответов «Нет». Количество ответов «Да» и «Нет» он записывал в журнал, но, к сожалению, часть записей была утеряна, как и информация об общем числе жителей.
Осведомитель из числа жителей сообщил ему два утверждения
1. В селе Лжецово вдвое больше жителей, чем в селе Хитрецово.
2. В сёлах Лжецово и Хитрецово разное число жителей, причём их количество отличается ровно в 2 раза.
Утверждения осведомителя могут быть либо истинными, либо ложными.
Ответьте на вопросы.
1. Сколько всего жителей живёт во всех трёх сёлах?
2. Сколько всего правдолюбов живёт в селе Правдино?
3. Сколько всего лжецов и хитрецов живёт в сёлах Лжецово и Хитрецово вместе?
4. Сколько лжецов живёт в селе Лжецово, если считать, что оба утверждения осведомителя оказались истинными?
5. Сколько хитрецов живёт в деревне Хитрецово, если считать, что оба утверждения осведомителя оказались ложными?
Ответ: 1)360 2)120 3)240 4)160 5)120
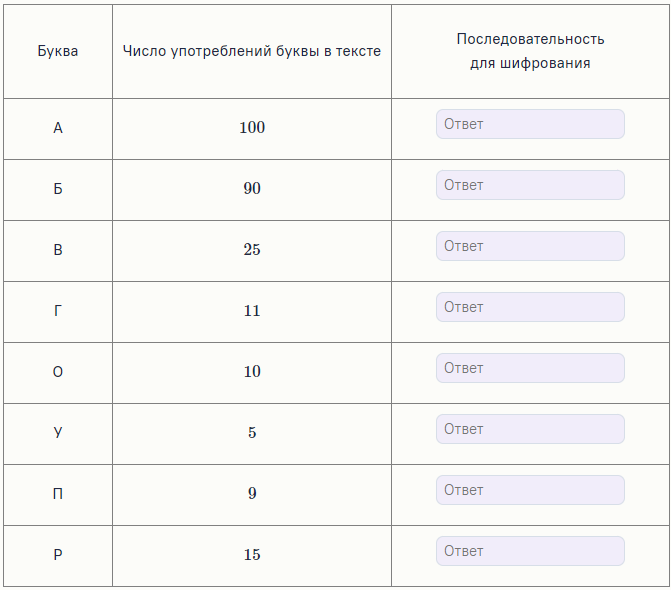
Задание 5. Азбука Морзе v2
Ваня недавно открыл для себя азбуку Морзе, где каждую букву можно представить в виде двух сигналов длинного (тире) и короткого (точка). Но его беспокоит, что без использования разделителя между отдельными буквами одно и то же сообщение можно расшифровать несколькими способами, поэтому Ваня начал размышлять, как можно усовершенствовать данную систему кодировки букв.
Ваня узнал, что для однозначной расшифровки сообщения нужно, чтобы ни одна последовательность точек и тире для одной буквы не была началом другой последовательности для другой буквы. Вооружившись этой идеей и подсчитав, сколько раз каждый символ встречается в тексте, Ваня задумался: как придумать такие кодовые слова для символов, чтобы закодировать текст с минимальным количеством точек и тире?
В таблице показано, сколько букв в тексте насчитал Ваня.
Помогите ему придумать для каждой буквы такую последовательность точек и тире, чтобы их суммарное количество, необходимое для кодирования текста, было минимальным. Обратите внимание: Ваня хочет, чтобы в дальнейшем данный текст можно было однозначно расшифровать.