25.10.2024 Школьный этап Сириус по Информатике вопросы и ответы для 7-8 класса

Задание 1. Робот‑пылесос
Робот пылесос каждую ночь проводит уборку на территории склада, схему которого вы можете видеть ниже: прямоугольное поле размером w×h разделено на квадратные секции. Зарядная станция робота, с которой он начинает своё движение, расположена в одном из углов склада. На уборку каждой секции робот затрачивает одну минуту, после чего перемещается на соседнюю. К сожалению для уборщика, для удобства хранения товаров склад разделён полками, расположенными «змейкой». Сквозь полки робот пройти не может, поэтому по ходу движения ему приходится проходить через некоторые секции дважды (и дважды там убираться). На рисунке такие секции обозначены звёздочками. По данным w и h определите время, которое робот пылесос затратит на уборку склада.

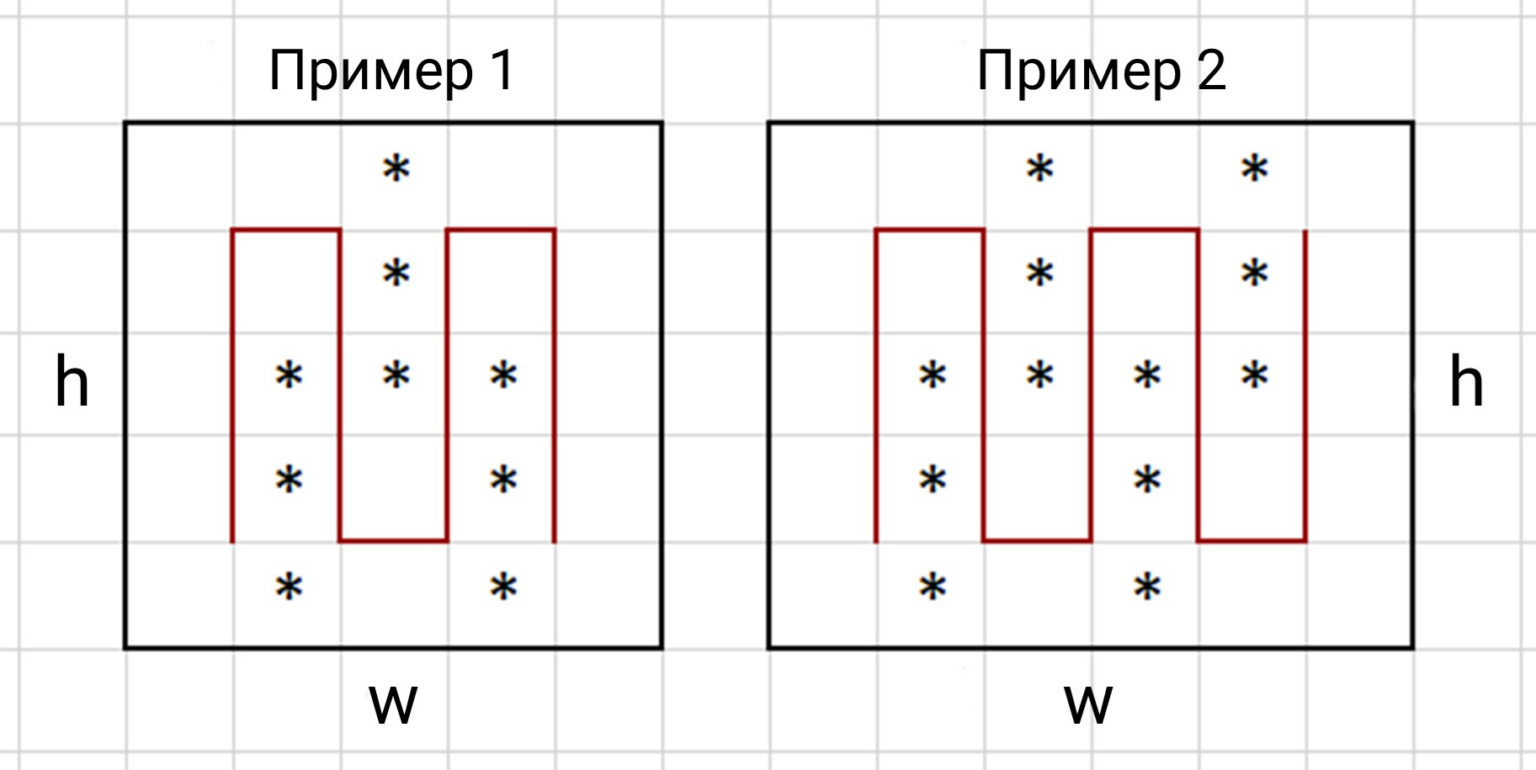
Ответом на эту задачу является некоторое выражение, которое может содержать целые числа, переменные w и h (обозначаются буквами английского алфавита), операции сложения (обозначаются +), вычитания (обозначаются −), умножения (обозначаются *) и круглые скобки. Запись вида 2w для обозначения произведения числа 2 и переменной w некорректна, нужно писать 2 * w.
Ваше выражение должно давать правильный ответ для любых натуральных значений w и h, больших 2. Например, для приведённых на первом рисунке w=5 и h=5 значение выражения должно быть равно 34, а для w=6 и h=5 на втором рисунке 42.
Пример правильной формы записи ответа: w * h−2 * (h−1)

Ответ = (W — 2)*(H — 2) + W*H

Задание 2. Маскарад
На школьном этапе ВсОШ по технологии участникам было предложено смоделировать и изготовить маску животного. С заданием успешно справились Белла, Захар, Егор и Харитон.
Поскольку тур олимпиады, на котором необходимо защищать проект, довольно продолжителен, для перекуса каждый из ребят принёс свой любимый «лесной» продукт питания: грибы, орехи, ягоды и фрукты. Участникам необходимо представить свою работу: маски медведя, орла, кенгуру и бегемота.

Известно, что: Харитон создал маску животного, впадающего в спячку. Харитон не любит есть грибы и фрукты. Белла и тот, кто принёс с собой орехи, создали маски хищников. Егор создал маску бегемота. Ни грибов, ни ягод у него с собой не было. Тот, кто создал маску орла, принёс с собой ягоды.
Определите, кто какую маску создал и что с собой принёс на перекус.

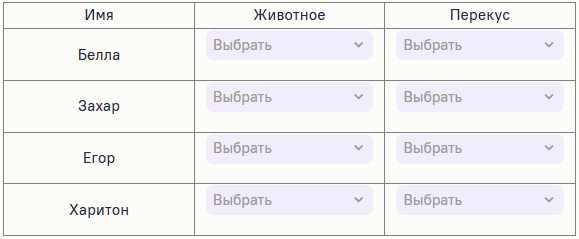
Животное: Медведь, Орел, Кенгуру, Бегемот
Перекус: Грибы, Орехи, Ягоды, Фрукты

Ответ:
Белла — маска орла, ягоды
Захар — маска кенгуру, грибы
Егор — маска бегемота, фрукты
Харитон — маска медведя, орехи

Задание 3. Разрезание строки
Сегодня на уроке информатики Данила узнал, что слова можно сравнивать в лексикографическом (алфавитном) порядке.
Лексикографический порядок слов  это способ их упорядочивания, аналогичный расположению в словаре. Сравнение слов при этом осуществляется по следующим правилам.
Сравнение букв: cначала сравниваются первые символы слов. Слово, первый символ которого стоит раньше в алфавите, считается меньшим. Например, слово «яблоко» будет стоять после слова «груша», потому что «я» стоит позже «г».
Длина слов: если два слова начинаются с одинаковых букв, то дальше сравниваются их символы по порядку. Если одно слово является префиксом другого (например, «кот» и «котёнок»), то более короткое слово считается меньшим, даже если они совпадают до определённой позиции.
Примеры: «собака» < «собачка», «дерево» < «долина», «апельсин» > «ананас». Такая система упорядочивания полезна для сортировки списков слов, поиска и обработки текстовой информации.
В процессе подготовки к олимпиаде по информатике Данила написал на полоске бумаги слово «СИРИУСОЛИМП», разрезал полоску в nn местах и переставил получившиеся куски местами (все получившиеся части исходного слова были использованы). Он мечтает сделать исходный «СИРИУСОЛИМП» как можно большим.
Ответьте на вопросы.
1) Какое наибольшее слово в лексикографическом порядке он может получить при n=1 (то есть сделав единственный разрез)?
2) Какое наибольшее слово в лексикографическом порядке он может получить при n=2?
3) Какое наибольшее слово в лексикографическом порядке он может получить при n=3?
4) Какое наименьшее количество разрезов необходимо сделать, чтобы получить из «СИРИУСОЛИМП» наибольшее лексикографическое слово?
Каждый верный ответ даст 25 баллов. Менее точные ответы будут оцениваться меньшим количеством баллов.
Буквы русского алфавита (для справки): А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я.

Ответ:

Длинное описательное условие, а ответ будет гораздо короче.

1) При одном разрезе: Самая старшая буква из всех предложенных это «У». С неё будет начинаться слово. Потому отрезаем перед ней и переставляем.

Потому будет слово

«УСОЛИМП | СИРИ»

2) При двух разрезах: Можно отрезать буквы «УС» и вставить перед первой «С»

Получим слово

«УС | СИРИ | ОЛИМП»

3) При трех разрезах: Отрезаем «УС» и ещё первую «С». И тогда можно вставить их в следующем порядке:

«УС | С | ОЛИМП | ИРИ»

4) Для решения сначала напишем это максимальное слово расставив буквы по не возрастанию

У — С — С — Р — П — О — М — Л — И — И — И

Из предложенной расстановки видим только возможные пары «УС» и «ЛИ» из начального слова, а все остальные по одной букве. Потому так и разрезаем считая с начала слова по одной букве и 2 раза по две.

Посчитаем, получим 8 разрезов.

Задание 4. Головоломка с простыми числами
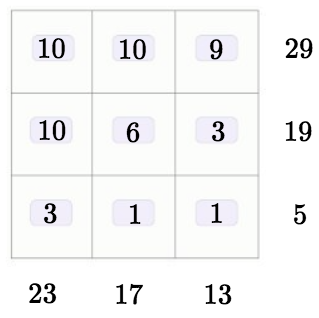
Для освоения темы «Простые числа» учитель математики Николай Николаевич предложил своим ученикам следующую задачу‑головоломку: в клетки таблицы 3×3 нужно расставить произвольные (возможно, повторяющиеся) целые числа от 0 до 10. После этого понадобится подсчитать суммы чисел в каждой из трёх строк и в каждом из трёх столбцов этой таблицы. Среди этих шести сумм нужно найти все простые числа и выписать каждое из них ровно по одному разу (то есть повторяющиеся простые числа не учитываются). Выигрывает тот ученик, у которого полученная сумма различных простых чисел окажется самой большой.
Рассмотрим пример. Один из учеников Николая Николаевича расположил в таблице числа следующим образом:

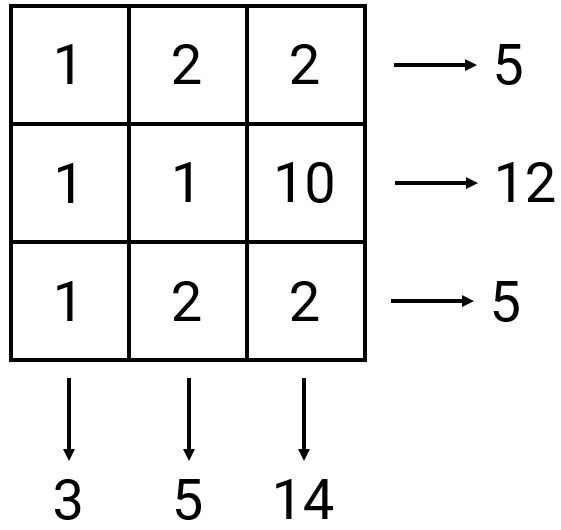
Среди полученных шести сумм по строкам и столбцам этой таблицы встречаются один раз простое число 3 и три раза простое число 5. Так как в итоге учитываются только различные простые числа, результат этого ученика равен сумме 3+5, то есть 8.
Вам предлагается поучаствовать в решении этой головоломки. Заполните ячейки в таблице целыми числами от 1 до 10. Далее проверяющая программа найдёт все суммы в вашей таблице по строкам и все суммы по столбцам и просуммирует все различные простые числа среди этих шести сумм. Чем больше окажутся значение этой суммы и количество различных простых чисел в ней, тем выше будет оценена попытка.
Замечание
Далее приводится список всех простых чисел, не превосходящих 50: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.

Ответ:

Сначала оценим некий максимум

Максимально можно получить среди сумм из 3 чисел от 0 до 10, это 10 + 10 + 10 = 30

Минимально соответственно 0 + 0 + 0 = 0

В диапазоне от 0 до 30: — десять различных простых чисел. А надо получить 6 различных и желательно максимально возможных.

А теперь давайте поймем что каждое число в ячейке участвует в сумме 2 раза (в строке и в столбце)

Таким образом сумма строк и сумма столбцов будет равна друг другу.

А сумма всех полученных чисел будет как раз суммой все столбцов и строк.

Тогда проверим максимально возможный вариант 29 + 23 + 19 + 17 + 13 + 11 = 112

Тогда в 3 строках и в 3 столбцах должно быть по 56 и это должна быть сумма 3-х нечетных простых. Такого не получится.

Заменим тогда 11 на меньшее 7

И следующая сумма 108 — тоже не годится.

А вот следующая сумма 106 = (29 + 23 + 19 + 17 + 13 + 5) или = (29 + 23 + 19 + 17 + 11 + 7)

Пополам будет по 53 и надо разделить по 3 простых в сумме по 53

Например 29 + 19 + 5 = 53 и 23 + 17 + 13 = 53

Расставляем эти числа в суммах строк и столбцов соответсвенно и заполняем числами квадрат.

Максимальное 10 + 10 + 9 = 29 — это например 1 строка

Ну а дальше произвольно чтоб суммы получались.

Например

Ответ: максимум 106

Задание 5. Всё могут короли!
Не могут они только стоять рядом друг с другом на шахматной доске (даже по диагонали). По размеру доски определите наибольшее количество королей, которое можно на ней расставить так, чтобы ещё одного короля поставить было невозможно.
Формат входных данных
Единственная строка входного файла содержит одно натуральное число nn (1≤n≤109) размер квадратной шахматной доски.
Формат выходных данных
Выведите одно натуральное число ответ на вопрос задачи.
Обратите внимание, что при заданных ограничениях для хранения входных данных и ответа может понадобиться 64‑битный тип данных, например, long long в C++, int64 в Free Pascal, long в Java.
Система оценки
Решения, верно работающие при 1≤n≤100, получат не менее 30 баллов.
Решения, верно работающие при 1≤n≤105, получат не менее 60 баллов.
Замечание
Смотри рисунок:

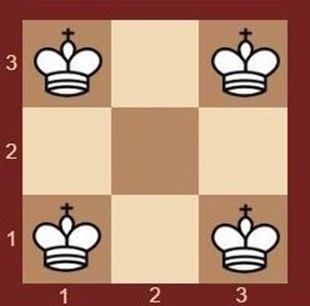
Ввод
3
Вывод
4

Ответ:

#include <iostream>

using namespace std;

int main(){

long long number;

cin >> number;

long long half = (number + 1) / 2;

cout << half * half;

}

Задание 6. Натуральный ряд
В научно‑исследовательском институте, где работает Тимофей, продолжается успешное исследование ряда натуральных чисел. Каждый день его коллеги открывают всё новые и новые свойства этой последовательности, и Тимофей старается от них не отставать. Сегодня Тимофей, как обычно, выписал на доске в ряд натуральные числа. Потом пришёл начальник отдела и стёр все числа, делящиеся на 2. Потом пришёл начальник другого отдела и стёр все числа из оставшихся, делящиеся на 3. Какое число теперь стоит на n-м месте в списке?
Формат входных данных
Единственная строка входных данных содержит натуральное число nn (1≤n≤109).
Формат выходных данных
Выведите одно натуральное число ответ на вопрос задачи.
Обратите внимание, что при заданных ограничениях для хранения входных данных и ответа может понадобиться 64‑битный тип данных, например, long long в C++, int64 в Free Pascal, long в Java.
Система оценки
Решения, верно работающие при 1≤n≤105, получат не менее 40 баллов.
Замечание
В примере дано n=5.
Из исходного ряда натуральных чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, …… сначала были удалены числа 2, 4, 6, 8, …… (как делящиеся на 2).
Остался ряд 1, 3, 5, 7, 9, 11, 13, 15, ……
Потом из него были удалены числа 3, 9, 15, …… (как делящиеся на 3).
Остался ряд 1, 5, 7, 11, 13, ……
На пятом месте число 13.
Ввод
5
Вывод
13

Ответ:

include <iostream> include <cmath> using namespace std;

int main() {

long long n;

cin >> n;

// Haxoдим п-ое число в ряду, где удалены числа, делящиеся на 2 и 3

long long count = 0;

long long num = 1;

while (count < n){

if (num % 2 != 0 && num % 3 != 0) {

count++;

if (count == n) {

break;

num += 2;

cout << num << endl;

return 0;

Задание 7. Городки
Городки старинная русская народная спортивная игра. В ней необходимо «выбивать» метанием биты различные деревянные фигуры, находящиеся на некотором расстоянии от игрока. Обычно участники самостоятельно приобретают комплекты для игры в спортивных магазинах, однако есть Очень Богатые Люди, готовые выложить за набор для игры из дорогих сортов древесины круглую сумму.
Начинающий предприниматель Тимофей заинтересовался этим перспективным бизнесом. Для организации официальных соревнований требуется изготовить для участников одинаковые биты, а для этого сначала необходимо где‑то раздобыть как можно больше одинаковых деревянных палочек. В распоряжении Тимофея есть палочки‑заготовки из дорогого красного дерева в форме цилиндров одинакового радиуса, но самой разной длины, из которых он и собирается изготовить биты.
Если длина палочки является чётным числом d, Тимофей может распилить её пополам и получить две палочки вдвое меньшей длины d2. Если же длина палочки является нечётным числом, Тимофей может распилить её на две части, как можно меньше отличающиеся друг от друга: ⌊d2(d пополам, округлённое вниз до целой части) и ⌈d2⌉ (d пополам, округлённое вверх до целой части). Распиливать уже распиленные ранее палочки Тимофею лень, и он переходит к следующей заготовке. Задача Тимофея получить наибольшее количество бит какого‑нибудь одного размера. Если таких размеров несколько, Тимофей выберет для организации соревнований наименьший.
Формат входных данных
В первой строке входных данных записано одно натуральное число: nn (1≤n≤105) длина самой длинной заготовки.
В следующих nn строках записано по одному натуральному числу didi (0≤di≤109, dn≠0) количество палочек длины i−1. Так, во второй строке записано количество палочек длины 1, в третьей количество палочек длины 2 и так далее. В последней строке записано количество палочек длины nn.
Обратите внимание, что при заданных ограничениях для хранения входных данных и ответа может понадобиться 64‑битный тип данных, например, long long в C++, int64 в Free Pascal, long в Java.
Формат выходных данных
Выведите в двух строках два натуральных числа наибольшее количество получившихся палочек одного размера и сам этот размер.
Система оценки
Решения, верно работающие при n≤3, получат не менее 30 баллов.
Решения, верно работающие при n≤1000, получат не менее 70 баллов.
Замечание
У Тимофея есть несколько палочек, самая длинная имеет длину 5. Более точно:
Нет палочек длины 1;
Одна палочка длины 2;
Нет палочек длины 3;
Одна палочка длины 4;
Две палочки длины 5.
Тимофей распилит пополам палочку длины 4 и получит две палочки длины 2. Также он распилит обе палочки длины 5 и получит две палочки длины 2 и две палочки длины 3. Вместе с имеющейся у него одной исходной палочкой длины 2 (её Тимофей пилить не будет) в его распоряжении окажется пять одинаковых палочек длины 2. Это наилучший результат, который может получить Тимофей (наибольшее количество палочек длины 1, которое можно получить из исходного набора, равно двум; палочек длины 3 двум; палочек длины 4 одному; палочек длины 5 двум).
Ввод
5
0
1
0
1
2
Вывод
5
2

Ответ:

n = int(input())
L = [0]

for i in range(n):
L.append(int(input()))

best_ans = 1
best_count = L[1]
if n > 1:
best_count += 2 * L[2]
if n > 2:
best_count += L[6 >> 1]

count = 1
i = 2
while count < n:
if i <= n:
count_cur = L[i]
if 2 * i + 1 <= n:
count_cur += L[2 * i + 1] + 2 * L[2 * i] + L[2 * i — 1]
elif 2 * i <= n:
count_cur += 2 * L[2 * i] + L[2 * i — 1]
elif 2 * i — 1 <= n: count_cur += L[2 * i — 1] if count_cur > best_count:
best_count = count_cur
best_ans = i

i += (n + 1)
i = i % n
count += 1

print(best_count)
print(best_ans)