Ответ
Задание 4. Сон Пифагора
Если во сне вы производите вычитание, то это свидетельствует о неразвитостивашей личности и неготовности жить своим умом! Любовь Поливалина, «Сонник Пифагора». Пифагору снится тревожный сон ему следует из числа nn постоянно вычитать его последнюю цифру, не равную нулю. Например, при n=27 Пифагор сначала получит число 27−7=20, потом 20−2=18, 18−8=10, 10−1=9, 9−9=0. Получив число 0, великий учёный избавится от кошмара, но проблема лишь в том, что ему снится очень большое число. Сколько вычитаний придётся совершить Пифагору, пока он не доберётся до нуля?
Формат входных данных
Единственная строка входных данных содержит натуральное число n (1≤n≤1018).
Формат выходных данных
Выведите одно натуральное число ответ на вопрос задачи.
Система оценки
Решения, правильно работающие при n≤105, будут оцениваться в 30 баллов.
Ввод
27
Вывод
5
Ответ:

Задание 5. Геометрическая игра на планшете
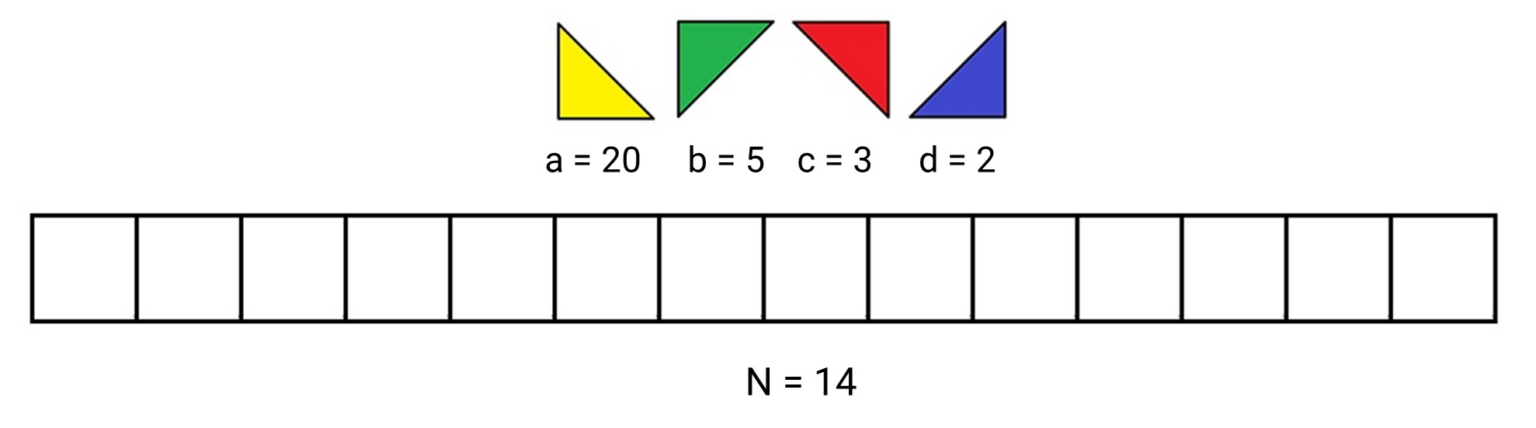
Маленький Андрей изучает геометрические фигуры при помощи игры на планшете. У него есть равнобедренные прямоугольные треугольники четырёх цветов и ориентаций: жёлтые, зелёные, красные и синие. Для каждой разновидности треугольников есть заданное количество экземпляров этих треугольников. Более точно, у Андрея есть a жёлтых, b зелёных, c красных и d синих треугольников. Известно, что a≥b≥c≥d. Все треугольники одинаковые по размеру, но у каждого есть своя ориентация, которую нельзя менять. Треугольники одного цвета имеют одну и ту же ориентацию.
Помимо этого, у мальчика есть n пустых ячеек, стороны которых совпадают с катетами треугольников. Игра происходит пошагово, на каждом шаге Андрей может взять очередной треугольник и переместить его параллельным сдвигом в одну из ячеек. При этом в одну ячейку можно поместить либо вместе жёлтый и красный треугольники, либо вместе зелёный и синий, либо один любой треугольник из имеющихся.
На каждом шаге можно переместить треугольник строго одного текущего цвета. Сначала это жёлтый, на следующем ходе зелёный, далее красный и затем синий. Далее снова жёлтый, зелёный, красный, синий и т.д по циклу. Если места для текущего цвета нет либо треугольники текущего цвета закончились, то этот цвет пропускается и ходит следующий по порядку цвет.
Допустим, в данном шаге есть треугольник текущего цвета. Если ещё есть пустая ячейка, данный треугольник обязательно помещается в эту ячейку. Если пустые ячейки закончились, но есть полупустая ячейка с парным текущему цветом, то треугольник помещается в неё. Игра длится до тех пор, пока есть цвет, который можно поместить в какую‑то ячейку.
Определите, сколько каких треугольников Андрей распределит в конечном итоге по ячейкам.
Формат входных данных
На вход подаются четыре числа a, b, c, d, каждое в своей строке. Гарантируется, что a≥b≥c≥da≥b≥c≥d. В пятой строке содержится число n количество пустых ячеек. 1≤a, b, c, d≤1018, 1≤n≤1018.
Обратите внимание, что значения переменных в этой задаче могут превышать возможные значения 32-битной целочисленной переменной, поэтому необходимо использовать 6464-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, long в Java и C#).
Формат выходных данных
Выведите ответ в четыре строки: для каждого соответствующего цвета укажите, сколько треугольников этого цвета получится поместить в ячейки. В первую строку выведите число жёлтых треугольников, во вторую зелёных, в третью красных и в четвёртую синих.
Система оценки
Решения, верно работающие при 1≤a, b, c, d, n≤1000, будут оцениваться в 30 баллов.
Решения, верно работающие при 4≤a+b+c+d≤106 и 1≤n≤106, будут оцениваться в 60 баллов.
Замечание
Для первого примера из условия проиллюстрируем некоторые промежуточные ситуации:
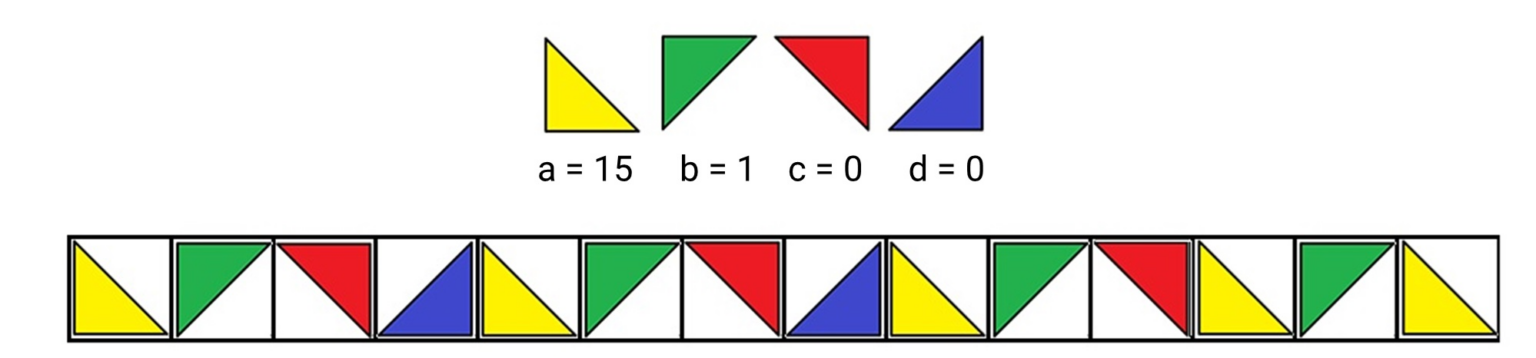
Положение после 14 первых ходов, если Андрей раскладывал треугольники по ячейкам слева направо. На данный момент закончились все пустые ячейки и треугольники красного и синего цветов.
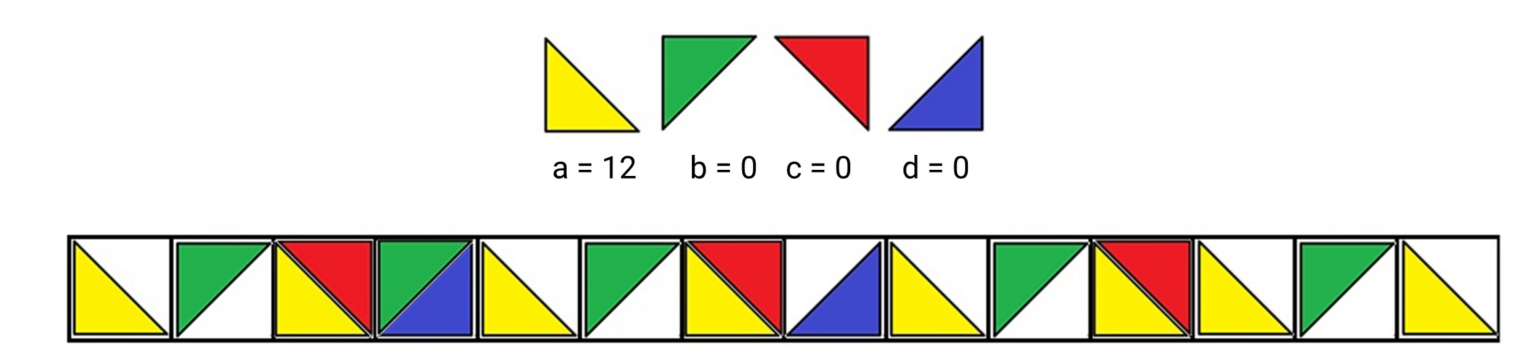
Итоговое положение после 18 ходов. Дополнительно получилось разложить ещё три жёлтых треугольника и один зелёный. Зелёные треугольники тоже закончились, а для жёлтых закончились места. Итого Андрей разложил 8 жёлтых, 5 зелёных, 3 красных и 2 синих треугольника.
Ввод
20
5
3
2
14
Вывод
8
5
3
2
Ввод
7
7
7
7
9
Вывод
5
4
5
4
