Математическая грамотность 9 класс 2024, задания и ответы?

Question

Математика ОБЖ Олимпиады Пословицы и поговорки

Вопрос. Полная версия

Ответ

Answer 1

Содержание

1. Дорога до дачи

Всем хорошо известно, как важны хорошие дороги, по которым можно в кратчайшие сроки перевозить необходимые грузы и перемещаться пассажирам. На автомобильной трассе М4 «Дон» в пределах Московского региона ввели в эксплуатацию три скоростных участка, на которых можно развивать скорость до 130 км/час. Скоростные участки трассы расположены от Москвы: первый – от отметки 51 км до отметки 71 км; второй – от отметки 76 км до отметки 103 км, третий – от отметки 113 км до отметки 120 км.

В субботу семья Ивановых выехала на автомобиле на дачу, которая расположена в 120 км от Москвы. В 8 ч утра они начали движение по трассе «Дон» и воспользовались скоростными её участками.

Задание 1. Определите, какие утверждения относительно характеристик движения автомобиля с дачниками являются верными.

Скоростные участки трассы обозначены на графике цифрами 2, 4 и 7
До первого скоростного участка трассы семья доехала за 45 минут.
За второй час поездки Ивановы проехали примерно 75 км.
Ивановы приехали на дачу в 12.00.

Задание 2. Опишите, что могло произойти на 100-м километре трассы. Ответ поясните.

Ответ: остановились отдохнуть

Задание 3. На участке трассы от отметки 71 км до отметки 76 км идут дорожные работы по соединению двух первых скоростных участков в единый скоростной участок. За какое наименьшее время можно будет преодолевать этот объединённый скоростной участок после завершения дорожных работ?

Ответ: 24 мин

Решение:

1) (103 – 51) : 130 = 0,4 (ч)

2) 0,4 · 60 = 24 (мин.)

2. Полочка в шкафу

Задание 1. Чтобы сделать полку в шкафу, Юра ищет кусок фанеры подходящего размера. Полка должна иметь форму прямоугольника со сторонами 22 см и 38 см. Один из друзей предложил ему лист фанеры в форме прямоугольной трапеции с основаниями 58 см и 35 см, высотой 24 см. Подойдёт ли этот лист? Юра попросил своих друзей – Кирилла, Ивана и Илью – помочь ему ответить на этот вопрос.

Мнения Кирилла и Ивана разошлись.

Кирилл: Я считаю, что лист фанеры подойдёт, если площадь листа фанеры больше площади полки.

Иван: Я считаю, что любой лист фанеры не подойдёт, если большая сторона полки больше, чем меньшее основание листа фанеры.

Согласны ли вы с аргументами ребят? Подчеркните нужное. Если не согласны, приведите контрпример.

Ответ:

Мнение Кирилла: Не согласен. Возможный контрпример: площадь трапеции равна (58 + 35) · 24/2 = 1116, площадь прямоугольника со сторонами 24 и 38 равна 24 · 38 = 912 Его площадь меньше площади трапеции, но он не поместится внутри трапеции.

Мнение Ивана: Не согласен. Возможный контрпример: прямоугольник со сторонами 38 и 12 поместится, хотя 38 > 35

Задание 2. Илья сделал чертёж и предложил такое решение: «Предположим, что наш прямоугольник, большая из сторон которого равна 38 см, разместился внутри трапеции так, что его вершина оказалась на боковой стороне трапеции. Найдём х − длину смежной стороны этого прямоугольника. Это наибольший из прямоугольников со стороной 38 см, который можно разместить внутри трапеции. Если смежная сторона прямоугольника больше х, то его разместить внутри трапеции нельзя. ВС – высота трапеции. Из подобия треугольников ABC и AKM находим x: Значит, прямоугольник со сторонами 38 и 22 см нельзя разместить внутри данной трапеции». Какие геометрические факты использовал Илья в своём решении? Отметьте все верные варианты ответа.

противоположные стороны прямоугольника равны
в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора)
если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны (первый признак подобия треугольников)
высота прямоугольной трапеции разбивает её на прямоугольник и прямоугольный треугольник
параллельные прямые отсекают на секущих пропорциональные отрезки (теорема Фалеса)

3. Игра в лото

При игре в лото используют непрозрачный мешок с деревянными бочонками, на торце каждого из которых нанесены числа от 1 до 90 За один ход ведущий наугад вынимает из мешка по одному бочонку и называет соответствующее число. У каждого игрока есть карточка в форме прямоугольника, разделённого на 3 горизонтальных и 9 вертикальных рядов, всего 27 ячеек. В каждом горизонтальном ряду расположено по 5 чисел в произвольном порядке, всего 15 чисел. Остальные клетки пустые. Игрок должен закрыть бочонками все ячейки с числами. Выигрывает тот, кто сделает это первым.

Задание 1. А) На карточке Тимофея одно однозначное число, остальные – двузначные. Какова вероятность того, что первым ходом ведущий вынет бочонок с любым однозначным числом? Б) Тимофей родился 15 декабря, поэтому считает число 15 своим счастливым числом. Какова вероятность того, что первым ходом ведущий вынет бочонок с числом, кратным 15?

Ответ: А) 9/90; Б) 6/90

Задание 2. На карточке Тимофея три числа с двумя одинаковыми цифрами – 22, 77 и 88 Ведущий делает первый ход. Какова вероятность того, что ведущий вынет бочонок с одним из этих чисел?

Ответ: 1/30.

4. Олимпийские медали

Как известно, олимпийские медали бывают разного достоинства: золотые, серебряные и бронзовые. На XXII Олимпийских зимних играх, которые прошли в 2014 году в Сочи, было вручено рекордное число серебряных медалей: 97 наград. Серебряные олимпийские медали, вручённые в Сочи, имеют диаметр 100 мм, толщину 10 мм и массу 525 граммов. Изготовлены эти медали из серебра 925 пробы.

Задание 1. А) Какова масса 97 серебряных медалей? Ответ дайте в кг. Результат округлите до целого. Б) Какова примерная масса серебра, израсходованного на изготовление одной серебряной медали XXII Зимних Олимпийских игр?

Ответ: А) 51 кг, Б) 486 г

Задание 2. Можно ли уложить эти 97 серебряные олимпийские медали во взломоогнестойком сейфе, характеристики которого даны в таблице?

Ответ: Да, можно.

Решение

600 : 10 = 60 – войдет 60 медалей по высоте сейфа

390 : 100 = 3,9 – войдет 3 медали по ширине сейфа

300 : 100 = 3 – войдет 3 медали по глубине сейфа

Всего может войти медалей: 60 · 3 · 3 = 540

5. Как измерить ширину реки

Саша готовится к туристическому походу, в котором придётся преодолевать водные преграды. Чтобы организовать навесную переправу, надо знать ширину реки. Как измерить ширину реки в походных условиях? В Интернете Саша нашёл несколько способов, как можно измерить ширину реки. Вот один из них: «Ширину небольшой реки можно измерять при помощи метода шагов. Оборудование: колышек, рулетка или мерная лента.

Алгоритм действий:

1 Встаньте у реки, лицом к противоположному берегу, это точка В.
2 Заметьте на противоположном берегу какой-либо ориентир, например,
дерево, это точка А.
3 Повернитесь направо на 90о и отсчитайте 50 шагов.
4 Установите второй ориентир, например, палку, это точка Е.
5 В том же направлении пройдите ещё 50 шагов, это точка С (отметьте её
колышком).
6 Снова развернитесь направо, как можно точнее сохраняя угол в 90о.
Начинайте движение, держа в поле зрения оба ориентира – А и Е.
7 Когда ориентиры окажутся на одной с вами линии, остановитесь, это
точка D.

Расстояние от точки С до точки D и будет шириной реки. Его можно измерить, например, рулеткой».

Задание 1. Действительно ли расстояние CD равняется ширине реки АВ? Докажите это.

Ответ: Вариант доказательства: В прямоугольных треугольниках АВЕ и DCE с прямыми углами В и С равны соответственно: катеты ВЕ и ЕС (по построению) и углы АЕВ и DEC (как вертикальные). Треугольники равны по второму признаку равенства прямоугольных треугольников по катету и прилежащему к этому катету углу. Из равенства треугольников следует, что АВ = DC.

Задание 2. У Саши нет рулетки необходимой длины, поэтому он решил измерить расстояние от точки С до точки D шагами. Саша узнал, что приближённо длину своего шага можно определить по формуле зависимости длины шага от роста. Воспользовавшись этой формулой, определите, чему будет равна ширина реки (в метрах), если от точки С до точки D Саша сделает 30 шагов. Рост Саши 180 см.

Ответ: 25 м

Решение:

1) Д = 1,8/4 + 0,37 = 0,82 (м)

2) 0,82 · 30 = 24,6 (м)

Задание 3. Выполняя измерения на местности, Саша столкнулся с неожиданным препятствием: от точки Е он смог сделать только 40 шагов, так как на его пути оказался заболоченный участок (см. рисунок ниже). Каким образом Саша может завершить свои измерения? Укажите способ, который он может применить, и приведите его обоснование.

Ответ: способ подобных треугольников. Построить треугольник ЕКМ, подобный ЕВА. Те же действия и построения на местности, при этом АВ находится из подобия, так: ВА/КМ = ВЕ/КЕ.

6. Стеллаж из ящиков

Из нескольких одинаковых ящиков в форме куба сделали стеллаж, изображённый на фото. Сторона куба равна 30 см.

Задание 1. Решено доработать стеллаж и сделать две дверцы, которые закрыли бы ниши, образованные стенками соседних ящиков. На фото они обозначены цифрами 1 и 2. Для каждой дверцы: а) укажите в таблице соответствующую её форме геометрическую фигуру: равносторонний треугольник, равнобедренный треугольник, квадрат, ромб, трапеция; б) вычислите длины сторон и величины углов выбранных фигур, занесите их в таблицу.

Ответ:

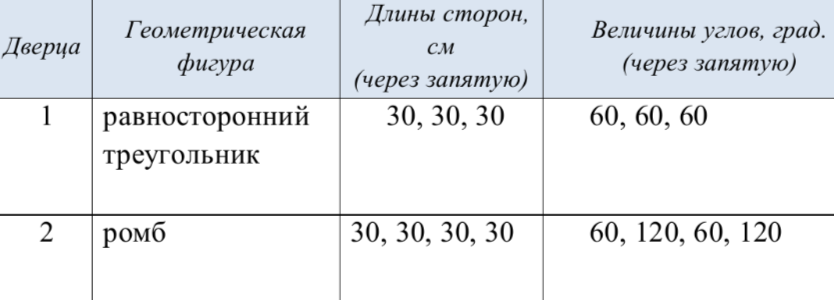
Задание 2. Можно ли разместить такой стеллаж в стенной нише, если высота ниши составляет 1 м?

Ответ: Да

Решение:

15 + 2 ∙ 15√3 + 30 = 45 + 30√3 (см) ≈ 97 (см)

97 см < 1 м.

7. Куриные яйца

По действующим российским стандартам маркировка должна быть на каждом яйце, произведённом на птицефабрике. Первый знак в маркировке означает допустимый срок хранения:

− буква «Д» обозначает диетическое яйцо, такие яйца реализуются в течение 7 дней;

− буква «С» обозначает столовое яйцо, которое реализуется в течение 25 дней. На яйце указывается дата его выпуска (дата сортировки).

Второй знак в маркировке означает категорию яйца в зависимости от его массы. На птицефабрике проводится сортировка партии куриных яиц по их массе и распределение по стандартным категориям. Доля яиц каждой категории (в %) в данной партии показана в таблице.

Задание 1. Для яйца, изображённого на фото, укажите дату, до которой яйцо должно было быть реализовано. Учтите, что в феврале 2013 года было 28 дней. Запишите дату следующим образом: ДД.ММ.ГГГГ – сначала запишите день (две цифры), затем – порядковый номер месяца в году (две цифры), в конце – год (четыре цифры).

Ответ: 02.03.13.

Задание 2. Какова средняя масса яиц данной партии? Ответ дайте в граммах. Результат округлите до целого.

Ответ: 58 г

Задание 3. Найдите вероятность того, что случайно выбранное из этой партии яйцо: А) относится к высшей категории; Б) имеет массу 55 и более граммов.

Ответ: А) 0,06 Б) 0,58.

8. Велосипедное колесо

Велосипедное колесо состоит из металлического обода, втулки со спицами и покрышки с камерой. При покупке покрышек для велосипеда их размер определяется по наружному диаметру металлического обода велосипедного колеса. На обод монтируется велосипедная покрышка с камерой. Обод велосипедного колеса изготавливают диаметром 10; 12; 16; 18; 20; 24; 26; 27,5; 28 или 29 дюймов.

Задание 1. Ниже показаны четыре вида велосипедов с разными диаметрами обода колеса. А) Велосипед какого вида сможет пройти наибольшее расстояние за один полный оборот обода? Б) Если перечисленные велосипеды будут двигаться в течение одного и того же количества времени с одинаковой постоянной скоростью, то обод колеса велосипеда какого вида сделает наибольшее количество оборотов во время езды?

Ответ: А) Спортивный велосипед Б) Детский велосипед.

Задание 2. Чтобы ехать на велосипеде, нужно крутить педали. Вращение педалей велосипеда обеспечивает вращение его колес. Составьте формулу для вычисления количества оборотов N велосипедного колеса, сделанных во время езды на велосипеде на расстоянии S (в см) с одинаковой постоянной скоростью, если диаметр обода d (в дюймах), а высота покрышки с камерой, установленной на обод, равна 2 см.

Ответ:

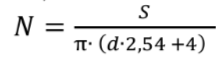
9. Конкур

Конкур — олимпийский конный вид спорта по преодолению препятствий, установленных в определённом порядке. Соревнования проходят на специальном поле для конкура. Выбирая лошадь для конкура, обращают внимание, прежде всего, на рост в холке и косую длину туловища. Для конкура эти характеристики должны удовлетворять условиям:

Нижняя допустимая граница высоты в холке – 167 см, верхняя – 177 см;
Косая длина туловища не должна быть меньше высоты в холке и не должна превышать её более чем на 4 см.

Задание 1. При подготовке рекомендаций специалистам, которые занимаются отбором лошадей для конкура, словесные формулировки заменяют на математические выражения. Запишите в виде двойных неравенств значения характеристик H и L, которые удовлетворяют условиям конкура.

Ответ: 167 ≤ Н ≤ 177, H ≤ L ≤ H+ 4

Задание 2. На конноспортивной базе несколько лошадей. Укажите в ответе номера тех из них, которые удовлетворяют условиям конкура.

Ответ: 1, 7

10. Деревенский колодец

Деревенский колодец представляет собой крытую бревенчатую шахту с воротом, к которому цепью крепится ведро. Ворот вращается ручкой. При вращении ручки ворот поворачивается, цепь постепенно наматывается на него, и ведро с водой поднимается на поверхность. За один поворот ручки ворот делает полный оборот вокруг оси, и на нём появляется один виток цепи. Диаметр ворота равняется обычно от 20 до 22 см.

Задание 1. А) При поднятии воды из колодца, диаметр ворота которого равен 20 см, сделали 20 оборотов ручкой. Высота деревянного сруба над землей – 80 см. Найдите глубину колодца (от уровня земли до уровня воды в колодце). Результат округлите до целого. Б) Запишите формулу для вычисления глубины колодца H (в м) в зависимости от диаметра ворота d (в м), количества оборотов n, высоты сруба l (в м).

Ответ: А) 12 м Б) Н= 3,14dn – l

Задача 2. Сколько оборотов ручкой необходимо сделать, чтобы поднять ведро с водой из колодца глубиной 9 м? Высота сруба колодца над землей – 80 см, диаметр ворота – 20 см.

Ответ: 16 оборотов

Решение:

1) 900 + 80 = 980 (см)

2) 3,14 ∙ 20 = 62,8 (см)

3) 980: 62,8 = 15,6

11. Закупка окон

Компания «Дом для семьи» занимается строительством коттеджных посёлков. Для остекления коттеджей она закупает у фирмы по изготовлению окон различные виды окон. Образцы окон с размерами в миллиметрах представлены на рисунках. Цены одного квадратного метра различных видов окон представлены в таблице ниже.

Задание 1. Отметьте «Верно» или «Неверно» для каждого утверждения в таблице, приведённой ниже.

Один квадратный метр треугольного окна дешевле одного квадратного метра прямоугольного окна на 2240 рублей. – Верно
Площадь одного окна в форме трапеции в 3 раза больше площади одного треугольного окна. – Неверно.

Задание 2. Фирма по изготовлению окон предоставляет покупателям следующие скидки: При заказе товара на сумму свыше 100 000 рублей предоставляется скидка 5%. При заказе товара на сумму свыше 300 000 рублей предоставляется скидка 10%. Какую сумму за покупку 20 прямоугольных окон заплатит строительная компания фирме с учётом скидок?

Ответ: 197 106 руб.

Решение:

1) 20 ∙ ((1,4 ∙ 1,3) ∙ 5700) = 207 480 руб.

2) 207 480 ∙ 0,95 = 197 106 руб.