Окружность с центром О вписана в треугольник АВС и касается его сторон АВ , ВС и АС в точках М, N и К соответственно.
Точка S, не лежащая в плоскости треугольника, удалена от каждой из точек касания на расстояние 9.
Найди периметр треугольника АВС, если его площадь равна 42, а расстояние от точки S до плоскости треугольника равно 3V5.
Ответ
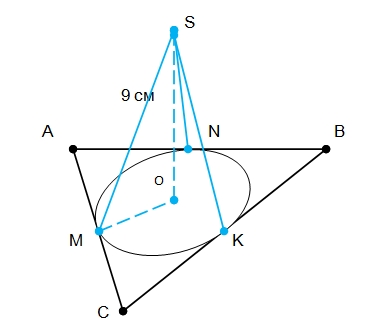
Так как, по условию, SM = SN = SK = 9 см, то точка S проецируется в точку О, центр вписанной окружности.
В прямоугольном треугольнике SOM, по теореме Пифагора, ОМ = r = SM^2 – OS^2 = 81 – 45 = 36.
ОМ = r = 6 см.
Радиус вписанной окружности равен:
r = S / p, тогда р = S / r = 42/6 = 7 см.
Равс = 2 * р = 2 * 7 = 14 см.
Ответ: Равс = 14 см.
