Ответ
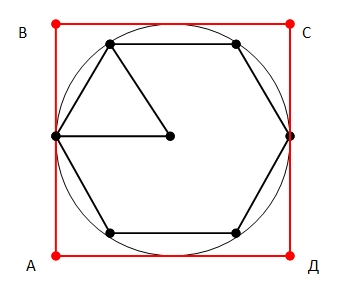
Пусть а – сторона правильного шестиугольника.
Зная площадь шестиугольника, определим длину его стороны.
S6 = 6 * (a^2 * √3/4) = 12 * √3.
а^2 = 48 / 6 = 8;
а = 2 * √2 cм.
Радиус описанной окружности около шестиугольника равен длине его стороны.
R = a = 2 * √2 cм.
Сторона квадрата, описанного около окружности, равна диаметру окружности.
АВ = 2 * R = 4 * √2 cм.
Тогда площадь квадрата равна:
Sкв = АB^2 = 32 см^2.
Ответ: Sкв = 32 см^2.
