В косоугольной системе координат с координатным углом 5pi/6 дана точка М(6;4). Найдите расстояние от этой точки до осей координат.

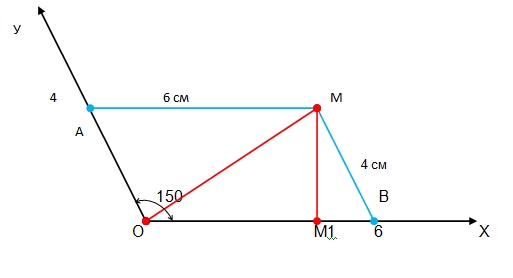
Построим систему координат ХОУ с углом ХОУ = 5 * π/6 = 150 и отметим точку О.
Четырехугольник АМВО параллелограмм со сторонами ОА = 4 см, ОВ = 6 см.
Расстояние от точки М до осей координат есть высоты параллелограмма.
Определим площадь параллелограмма.

S = ОА * ОВ * Sin150 = 4 * 6 * (1/2) = 12 см^2.

Так же S = ОА * ОМ.

ОМ = S / ОА = 12/4 = 3 см.

Так же S = ОВ * ММ1.

ММ1 = S / ОВ = 12/6 = 2 см.

Ответ: 2 см и 3 см.