Ответ
Задание 1. Костя начал выписывать в порядке возрастания все числа, для которых одновременно выполняются следующие условия: состоят только из цифр 5 и 8; имеют столько же пятёрок, сколько восьмёрок; делятся на 3.
Какое число у Кости стоит на втором месте?
Задание 2. Дима отправился гулять по квадрату 200×200, от правого верхнего угла к центру. Сперва он идёт по верхней строке до второго столбца, поворачивает налево, доходит до третьей снизу строки, поворачивает налево, доходит до четвёртого справа столбца и т. д., пока не окажется в одной из четырёх центральных клеток. На рисунке изображён такой путь для доски 8×8, и он состоит из 16 клеток.

Определите длину пути для доски 200×200.
Задание 3. Имеется 9 коробок, в каждую из которых положили синие и красные шарики, так что в каждой коробке есть хотя бы один синий и хотя бы один красный шарик. Коля нашёл разницу между количеством шариков разных цветов в каждой коробке (если они не равны, то из большего вычел меньшее). Эти числа написал на коробках. Оказалось, что было написано 9 разных чисел. Какое минимальное количество шариков может лежать суммарно во всех коробках, если известно, что общее количество красных шариков такое же, как общее количество синих?
Задание 4. В одной комнате собрались 5 девочек: Аня, Белла, Вера, Галя и Даша и подсчитали количество съеденных ими за неделю конфет. Оказалось, что если из комнаты выйдет Аня, то среднее арифметическое количества съеденных за неделю конфет четырёх оставшихся девочек будет равно 59. Аналогично без Беллы это число будет равно 53, без Веры 57, без Гали 56, без Даши 45.
Как зовут девочку, которая съела больше всего конфет за эту неделю?
Аня
Белла
Вера
Галя
Даша
Сколько конфет она съела?
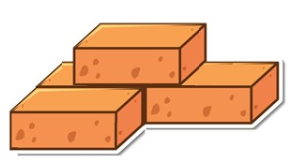
Задание 5. Из четырёх одинаковых кирпичей сложили конструкцию, как показано на рисунке. Известно, что суммарная площадь поверхности этой конструкции (сверху, снизу, со всех боков) равна 816 см2. Найдите площадь поверхности одного кирпича. Ответ выразите в квадратных сантиметрах.
Определите длину пути для доски 200×200.
Задание 6. Барабашка живёт в раздевалке, где стоят шкафчики с номерами от 73 до 89. Однажды ночью Барабашка занялся колдовством: он стал произносить вслух числа натурального ряда, начиная с 1. При этом, если номер шкафчика делится на называемое число, то шкафчик подпрыгивает один раз, в противном случае стоит смирно. Безобразия прекратились, как только было произнесено число, в ответ на которое ни один шкафчик не среагировал. Какое это было число? Шкафчик с каким номером подпрыгнул наибольшее число раз?
Задание 7. На дне рождения у Дядьки Черномора присутствовали все 33 богатыря. Черномор угощал их тортом по очереди. Первый богатырь съел 1/4 всего торта, второй 1/5 оставшегося, третий 1/6 оставшегося и так далее. Наконец 3-й богатырь съел 1/36 оставшегося куска, и то, что осталось, съел Черномор. Кто съел больше: первый богатырь или Черномор? Во сколько раз? Если богатырь и Черномор съели поровну, в ответ запишите 1
Задание 8. Муми‑мама испекла три одинаковые пиццы в виде правильного шестиугольника и сложила их рядом, как показано на рисунке.
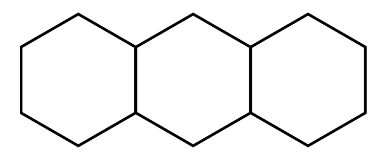
Муми‑тролль сделал два прямых разреза, как на рисунке, и взял себе кусочек, отмеченный красным.
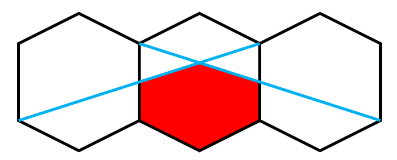
Какую часть одной пиццы взял себе Муми‑тролль?
