Ответ
Задание 1. Стена
При возведении стены крайне важно заказать ровно нужное количество кирпичей. Это количество можно вычислить. Разработайте формулу для расчёта необходимого количества целых кирпичей для стены длиной L метров и высотой H метров (L, H натуральные числа), принимая, что длина одного кирпича составляет 25 сантиметров, а высота 5 сантиметров. При укладке кирпичей в несколько рядов каждый следующий ряд смещается на половину кирпича (см. рисунок). Половинки кирпичей учитывать не нужно, так как их на складе и так очень много. Толщиной раствора между кирпичами можно пренебречь.
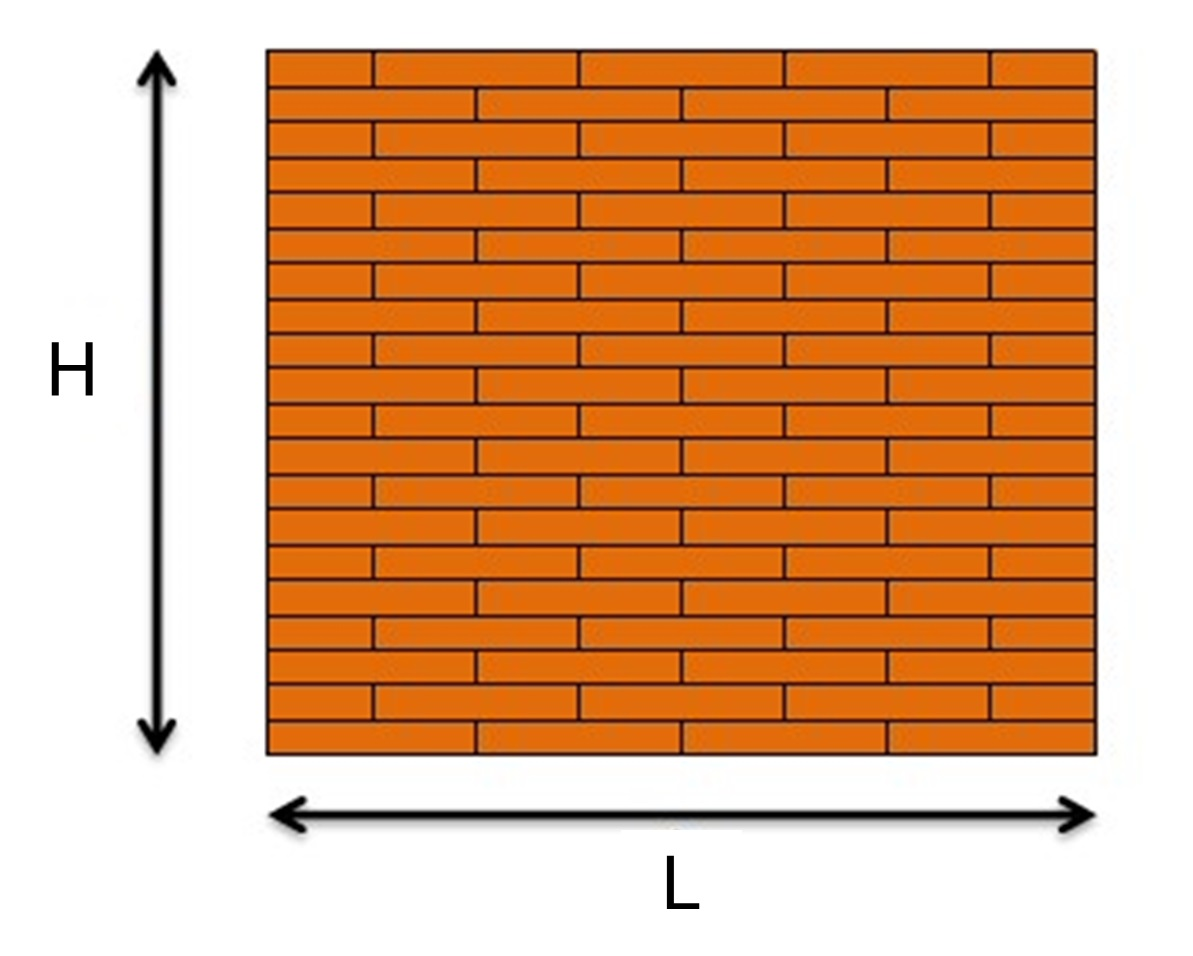
Ответом на эту задачу является некоторое выражение (формула), которое может содержать целые числа, переменные L и H (обозначаются заглавными английскими буквами), операции сложения (обозначаются «+»), вычитания (обозначаются «−»), умножения (обозначаются «*»), деления (обозначаются «/») и круглые скобки. Запись вида 2H для обозначения произведения числа 2 и переменной H некорректна, нужно писать 2 * H.
Ваше выражение должно давать правильный ответ для любых натуральных значений L и H. Например, для приведённых на рисунке L=1 и H=1 значение выражения должно быть равно 70. Пример правильной формы записи ответа: H * L−2 * (L−1) +4
Ответ: 10*Н*(8*L-1)
Задание 2. Правда или ложь
Рядом с Кудыкиной горой есть три села: Правдино, Лжецово и Хитрецово. Достоверно известно, что в селе Правдино живут только правдолюбы, в селе Лжецово лжецы, а в селе Хитрецово хитрецы, которые не хотят, чтобы их обложили налогами, поэтому всегда лгут о своём местоположении, а обо всём остальном могут говорить и правду, и ложь.
Переписчик Иванов пошёл на хитрость: он опросил всех жителей, задавая каждому лишь три вопроса:
1. Ты из села Правдино?
2. Ты из села Лжецово?
3. Ты из села Хитрецово?
На первый вопрос он получил 360 ответов «Да», на второй вопрос и третий вопросы вместе 480 ответов «Нет». Количество ответов «Да» и «Нет» он записывал в журнал, но, к сожалению, часть записей была утеряна, как и информация об общем числе жителей.
Осведомитель из числа жителей сообщил ему два утверждения
1. В селе Лжецово вдвое больше жителей, чем в селе Хитрецово.
2. В сёлах Лжецово и Хитрецово разное число жителей, причём их количество отличается ровно в 2 раза.
Утверждения осведомителя могут быть либо истинными, либо ложными.
Ответьте на вопросы.
1. Сколько всего жителей живёт во всех трёх сёлах?
2. Сколько всего правдолюбов живёт в селе Правдино?
3. Сколько всего лжецов и хитрецов живёт в сёлах Лжецово и Хитрецово вместе?
4. Сколько лжецов живёт в селе Лжецово, если считать, что оба утверждения осведомителя оказались истинными?
5. Сколько хитрецов живёт в деревне Хитрецово, если считать, что оба утверждения осведомителя оказались ложными?
Ответ:
1)360
2)120
3)240
4)160
5)120
Задание 3. Азбука Морзе v2
Ваня недавно открыл для себя азбуку Морзе, где каждую букву можно представить в виде двух сигналов длинного (тире) и короткого (точка). Но его беспокоит, что без использования разделителя между отдельными буквами одно и то же сообщение можно расшифровать несколькими способами, поэтому Ваня начал размышлять, как можно усовершенствовать данную систему кодировки букв.
Ваня узнал, что для однозначной расшифровки сообщения нужно, чтобы ни одна последовательность точек и тире для одной буквы не была началом другой последовательности для другой буквы. Вооружившись этой идеей и подсчитав, сколько раз каждый символ встречается в тексте, Ваня задумался: как придумать такие кодовые слова для символов, чтобы закодировать текст с минимальным количеством точек и тире?
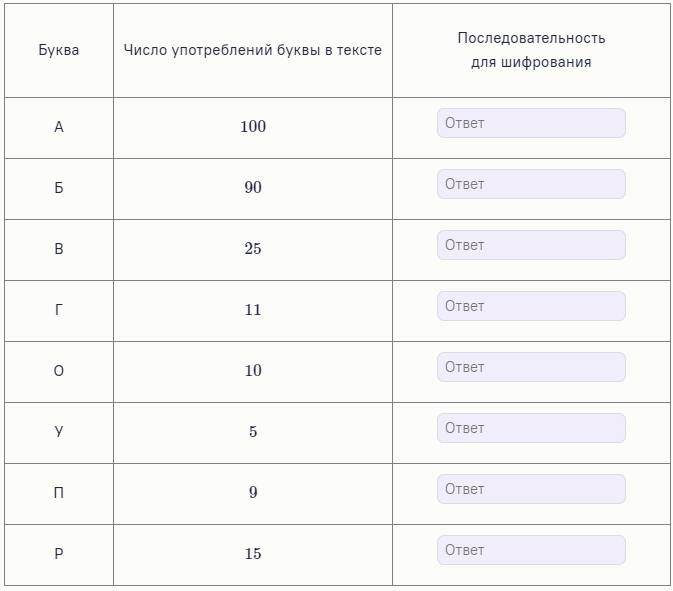
В таблице показано, сколько букв в тексте насчитал Ваня.
Помогите ему придумать для каждой буквы такую последовательность точек и тире, чтобы их суммарное количество, необходимое для кодирования текста, было минимальным. Обратите внимание: Ваня хочет, чтобы в дальнейшем данный текст можно было однозначно расшифровать.
Задание 4. Поезда
Ваня очень любит поезда и часто проводит время на железнодорожной станции, наблюдая за их движением. Однажды ему в руки попалось расписание поездов, и он решил разобраться, как устроена работа станции.
Помогите Ване ответить на несколько вопросов.
Для выполнения задания вы можете использовать электронные таблицы из офисного пакета или любые другие средства вашего компьютера. Данные находятся в файле, который вы можете скачать в одном из двух форматов: Microsoft Excel (XLSX) или LibreOffice Calc (ODS).
В этой таблице в столбце с данными B содержится время прибытия поездов, а в столбце с данными C время их отправления. Все данные в этих столбцах заданы в 24-часовом формате ЧЧ:MM, где Ч часы, M минуты. В момент прибытия и отправления поезд считается находящимся на станции. И обратите внимание, что некоторые поезда могут прибывать на станцию до полуночи, а отбывать уже после полуночи на следующий день.
Если вы не знаете ответ на какой‑либо вопрос, запишите вместо него любое число.
1. Сколько минимально путей должно быть на станции, чтобы на них могли находиться все поезда, не мешая друг другу в течение всего дня?
2. В какой период времени на станции находится наибольшее количество поездов одновременно? Ответ запишите в минутах.
3. В течение какого времени за сутки на станции нет ни одного поезда? Ответ запишите в минутах.
4. Ваня хочет выбрать самое интересное время для наблюдений. Сколько поездов будет на станции ровно в 10:00?
Задание 5. Мастер‑класс
Антон Алексеевич, преподаватель математики в старшей школе, решил продемонстрировать практическое применение математических расчётов и провести мастер‑класс по очистке квадратной маркерной доски длины n квадратной губкой длины a.
Антон Алексеевич использует свой фирменный метод, затирая каждый сантиметр доски без лишних движений. Он начинает с верхнего левого угла доски, двигаясь слева направо, затем вниз, влево, вверх, повторяя этот процесс, пока вся доска не будет очищена, но не проходя губкой по тем местам, которые уже очищены (см. рисунок ниже). Губка не вращается во время стирания с доски. Гарантируется, что длина стороны губки делит длину стороны доски без остатка.
Определите длину ломаной линии, которую описывает верхний левый угол квадратной губки при затирании квадратной доски.
Формат входных данных
Первая строка содержит целое число n (1≤n≤109) длину стороны доски.
Вторая строка содержит целое число a (1≤a≤109, a≤n) длину стороны губки. nn делится на a без остатка.
Формат выходных данных
В единственной строке выведите число длину ломаной, которую пройдёт левый верхний угол губки.
Обратите внимание, что ответ в этой задаче может превышать возможное значение 32‑битной целочисленной переменной, поэтому необходимо использовать 64‑битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, тип long в Java и C#).
Система оценки
Решения, правильно работающие при n, a≤103, будут оцениваться в 40 баллов.
Замечание
Проиллюстрируем пример к условию. Жёлтым на схеме обозначена губка, голубым очищенная область, красным маршрут левого верхнего угла губки.
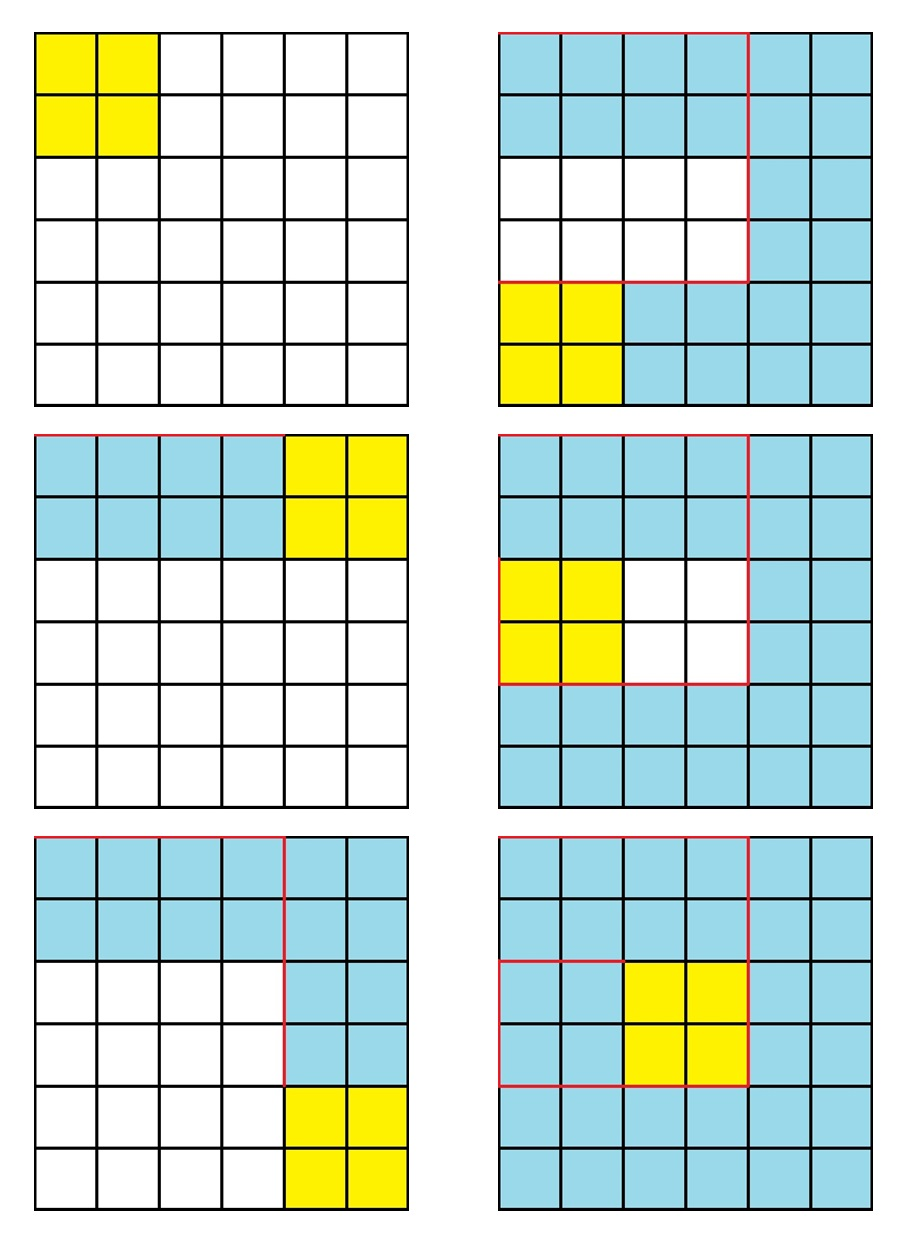
Ввод
6
2
Вывод
16
Ответ:
Язык Python 3
a = int(input())
b = int(input())
d = int(b)
if b > 1:
4пробелаb = b**2
4пробелас = (a**2 // b) – 1
4пробелас = c * d
else:
4пробелаb = b**2
4пробелас = (a**2 // b) – 1
print(c)
Задание 6. Наши слоны
На столе лежит шахматная доска, в которой n строк и m столбцов. Слон может ходить по диагонали на любое количество клеток. Пустая клетка находится «под боем», если какой‑либо из слонов на доске может одним ходом перейти на эту клетку. На доске в четырёх углах стоят четыре слона. Сколько клеток находится «под боем»?
Формат входных данных
В первой строке содержится количество строк шахматной доски nn, во второй столбцов mm (2≤n, m≤108).
Формат выходных данных
В единственной строке выведите целое число количество клеток, находящихся «под боем».
Система оценки
Решения, правильно работающие при nn, m≤500, будут оцениваться в 52 балла.
Замечание
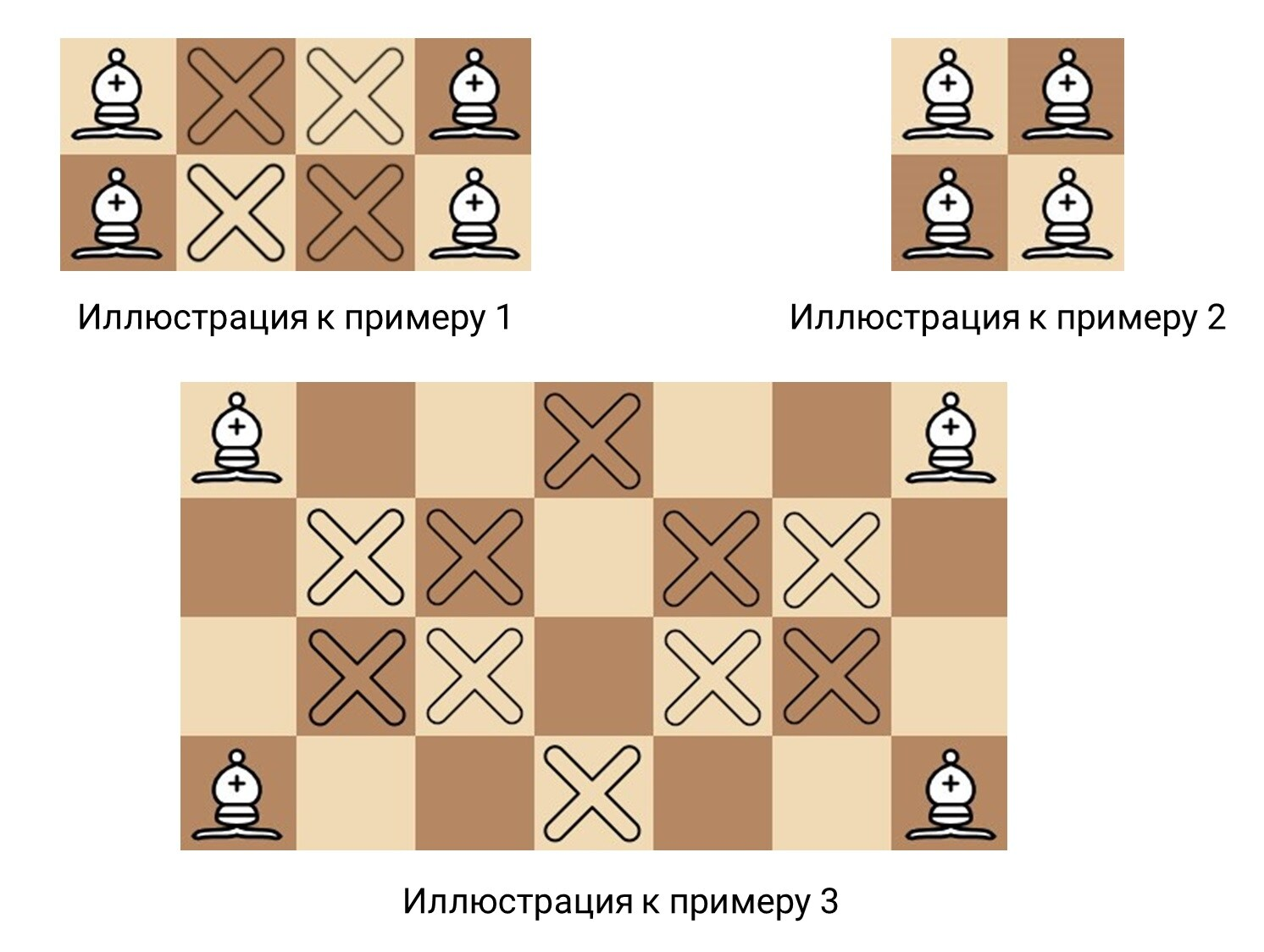
Ввод
2
4
2
2
4
7
Вывод
4
0
10
Ответ:
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <random>
using namespace std;
int main() {
int n, m; cin >> n >> m;
if (n > m) swap(n, m);
if (n == m) cout << 2 * n — n % 2 — — 4; else {
int ans = 4 * (n — 1);
if (n % 2) ans -= 2;
if (m % 2 && 2 * n — 1 >= m) ans -= 2;
cout << ans;
}
Задание 7. Пирамидки
Ваня хочет построить из кубиков n пирамидок. Он собирает пирамидки следующим образом:
1. Изначально в каждой пирамидке имеется по a1 кубиков в первом ряду.
2. В каждой второй пирамидке, т.е. номер которой делится на 2, к ним добавляется по a2 кубиков во второй ряд.
3. В каждой четвёртой пирамидке, т.е. номер которой делится на 4, добавляется по a3 кубиков в третий ряд.
4. В каждой восьмой пирамидке, т.е. номер которой делится на 8, добавляется по a4 кубиков в четвёртый ряд.
И так далее.
Выразим условие более формально: в каждой пирамидке, номер которой делится на (i−1)-ую степень числа 2, к исходному числу кубиков a1 добавляется по ai кубиков в i ряд. Помогите Ване определить количество кубиков, которое ему нужно для построения всех пирамидок.
Формат входных данных
Первая строка входных данных содержит число nn (1≤n≤109) количество пирамидок, которые хочет построить Ваня.
Вторая строка входных данных содержит число kk (1≤k≤30) количество рядов, для которых известно, сколько в них будет кубиков. Гарантируется, что в каждой пирамидке не более чем k рядов.
Каждая из следующих k строк содержит aiai (1≤ai≤109) количество кубиков в i-м ряде пирамидки. Количество кубиков, требующихся для каждого следующего слоя, не убывает.
Формат выходных данных
В единственной строке выведите число количество кубиков, которые нужны Ване для постройки всех пирамидок.
Обратите внимание, что ответ в этой задаче может превышать возможное значение 32‑битной целочисленной переменной, поэтому необходимо использовать 64‑битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, тип long в Java и C#).
Система оценки
Решения, правильно работающие при n≤15, ai≤100, будут оцениваться в 20 баллов.
Решения, правильно работающие при n≤105, будут оцениваться в 50 баллов.
Замечание
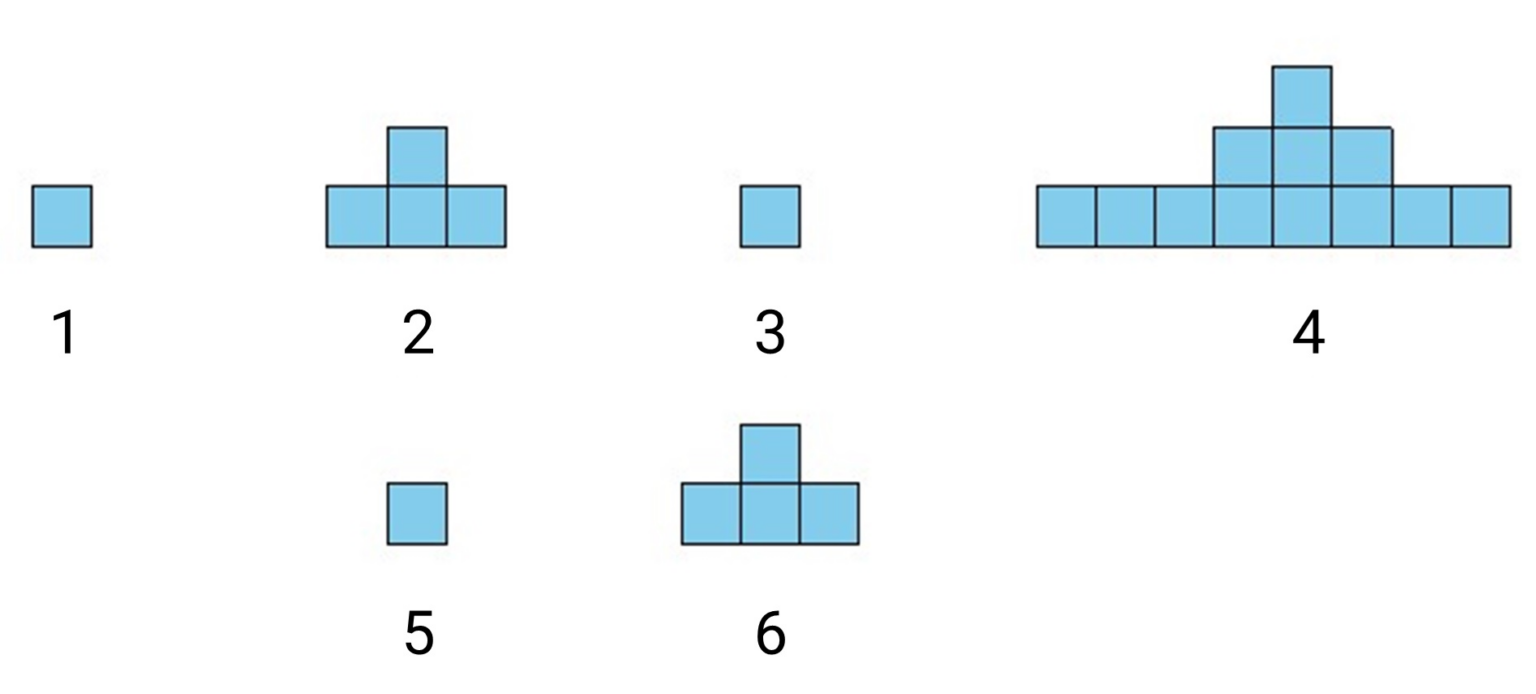
Рассмотрим первый пример. Пирамидки с нечётными номерами 1, 3, 5 имеют по одному ряду и состоят из 1 кубика. Пирамидки с номерами 2, 6 имеют по два ряда и состоят из 1+3 кубиков. Пирамидка с номером 4 имеет 3 ряда и состоит из 1+3+8 кубиков. В сумме Ване потребуется 1+(1+3)+1+(1+3+8)+1+(1+3) = 23 кубика. Пирамидки изображены на рисунке.
Ввод
6
3
1
3
8
Вывод
23
63
