25.10.2024 Школьный этап Сириус по Информатике вопросы и ответы для 5-6 класса

Задание 1. Города
Города словесная игра для нескольких человек. Каждый участник по очереди называет город, причём его название должно начинаться на ту же букву, которой оканчивается название города, озвученное предыдущим игроком. Например, за Сочи (последняя буква в названии и) может последовать Ижевск и т.д.
Сегодня, 25 октября 2024 года, задачи школьного этапа олимпиады по информатике решают участники из четвёртой группы регионов, в которую входят 20 областей, краёв и республик. Попробуйте из названий их столиц составить как можно более длинную цепочку (в информатике такая структура данных называется линейным двусвязным списком) для игры в города. Для определённости считайте, что если название населённого пункта пишется через дефис, то оно начинается с первой буквы первого слова и заканчивается последней буквой второго слова. В игре используются все буквы русского алфавита.
Расположите города в подходящем порядке. Чем длиннее будет ваша цепочка, тем больше баллов вы получите. Оцениваться будут только наборы названий городов, удовлетворяющие требованиям. Начать можно с любого населённого пункта из списка.
Абакан
Анадырь
Барнаул
Биробиджан
Благовещенск
Владивосток
Горно-Алтайск
Иркутск
Кемерово
Красноярск
Кызыл
Магадан
Новосибирск
Петропавловск-Камчатский
Томск
Улан-Удэ
Хабаровск
Чита
Южно-Сахалинск
Якутск

Ответ: Чита, Абакан, Новосибирск, Красноярск, Кемерово

Задание 2. Первое сентября
Три подружки Маша, Таня и Даша на первое сентября купили себе платья белого, красного и жёлтого цветов. Чтобы хорошо сочетаться друг с другом, они решили надеть банты таких же цветов. Известно, что: Цвет платья и банта не совпадает у каждой девочки. У Даши и Тани платье и бант белого цвета, но неизвестно, у кого что. У Маши и Тани платья красного и жёлтого цветов. Бант Даши и платье Маши красного цвета.
Определите цвет банта и платья для каждой девочки.

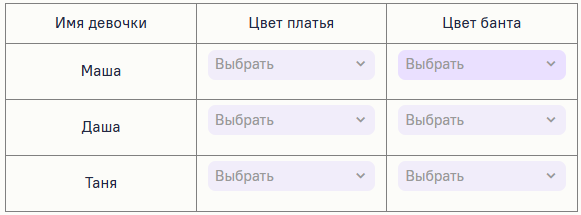
Цвет платья: Белый, Жёлтый, Красный
Цвет банта: Белый, Жёлтый, Красный

Ответ:
Маша = красное платье, желтый бант
Даша = белое платье, красный бант
Таня = желтое платье, белый бант

Задание 3. Разрезанное число
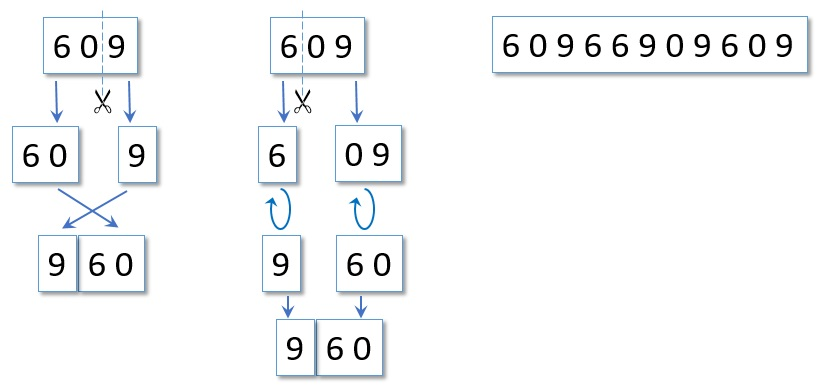
У Тимофея есть полоска бумаги, на которой записано число 60966909609 (нетрудно заметить, что в его записи используются только цифры 0, 6 и 9). Мальчик хочет разрезать это число на две части и соединить их так, чтобы получилось как можно большее число. При этом каждую из двух получившихся частей можно переворачивать на 180 градусов и соединять в любом порядке.

Например, если бы у мальчика было число 609, то он смог бы получить из него число 960, причём двумя способами.
Во‑первых, можно просто разрезать число на две части (60 и 9) и переставить их местами.
Во‑вторых, можно разрезать число по‑другому (6 и 09). Перевернём 6 получим 9, перевернём 09 получим 60. Соединим части в том же порядке получим 960.
Какое наибольшее число может получить Тимофей?

К проверке будут приниматься только числа, которые возможно получить из исходного числа описанными способами. Чем больше будет ваше число, тем больше баллов вы получите

Задание 4. Сок
В бочке 12 литров сока. С помощью четырёх ёмкостей объёмами 3, 5, 6 и 7 литров нужно разделить сок между тремя людьми так, чтобы у каждого была ёмкость (или бочка) с одинаковым количеством сока. Как это сделать?
От вас требуется составить как можно более короткий алгоритм распределения сока. Обозначим ёмкости 3, 5, 6 и 7 л буквами A, B, C и D соответственно, а 12-литровую бочку буквой Z. Для записи алгоритма используются команды вида X>Y (вместо X и Y используйте два различных символа из A, B, C, D), которые означают, что из ёмкости X происходит переливание сока в ёмкость Y. Команды записываются по одной в строке. Например, следующая последовательность команд:Z>B, Z>D, B>A, D>C, означает, что из бочки переливается сок в пятилитровую ёмкость, затем из бочки сок переливается в семилитровую ёмкость, затем из ёмкости вместимостью 5 л сок переливается в ёмкость объёмом 3 л, затем из ёмкости вместимостью 7 л сок переливается в шестилитровую ёмкость. После такой последовательности команд мы имеем 3+2+6+1=12 литров сока во всех ёмкостях.
Обратите внимание нельзя перелить сок в количестве, не соответствующем свободному объёму хотя бы одной тары. Например, из полной семилитровой ёмкости нельзя перелить три литра в пустую шестилитровую. А вот если в шестилитровой уже есть три литра сока, то добавить ещё три можно.
Оцениваться будут только решения, которые приводят к поставленной цели. Чем меньше шагов окажется в вашем алгоритме, тем больше баллов вы получите. За самый короткий алгоритм вы получите 100 баллов. За каждую избыточную команду будет сниматься по 15 баллов. Решения, в которых обнаружится некорректная команда (попытка перелить из пустой ёмкости, попытка перелить в полную ёмкость или попытка перелить из одной ёмкости в ту же самую), оцениваются в 0 баллов.

Задание 5. Многообещающая дата
Старик Хоттабыч называет дату многообещающей, если все цифры в её записи различны. При этом дата записывается в формате dd.mm.yyyy с ведущими нулями. Например, пятнадцатое марта 2025 года запишется как 15.03.2025. Эта дата не будет многообещающей, так как в её записи несколько раз встречаются цифры 0 и 2. А вот дата пятнадцатое марта 2469 года будет многообещающей в её записи 15.03.2469 все цифры различны.
Считайте, что количество дней в месяце определяется по принятым сейчас правилам:28 дней в феврале невисокосного года;
29 дней в феврале високосного года;
30 дней в апреле, июне, сентябре, ноябре;
31 день в январе, марте, мае, июле, августе, октябре и декабре.
Ответьте на следующие вопросы.
1) Сегодня 25 октября. В каком ближайшем году эта дата будет многообещающей?
2) Когда была последняя многообещающая дата?
3) Когда будет следующая многообещающая дата?
4) Сколько многообещающих дат было в 1875 году?
5) Какое наибольшее количество многообещающих дат может быть в календарном году при условии, что в его записи используется ровно четыре цифры?
Если вы не можете ответить на какой‑то вопрос, то запишите в соответствующем поле любое положительное число. За каждый правильный ответ вам будет начислено по 20 баллов.