Для освоения темы «Простые числа» учитель математики Николай Николаевич предложил своим ученикам следующую задачу‑головоломку: в клетки таблицы 3×3 нужно расставить произвольные (возможно, повторяющиеся) целые числа от 0 до 10. После этого понадобится подсчитать суммы чисел в каждой из трёх строк и в каждом из трёх столбцов этой таблицы. Среди этих шести сумм нужно найти все простые числа и выписать каждое из них ровно по одному разу (то есть повторяющиеся простые числа не учитываются). Выигрывает тот ученик, у которого полученная сумма различных простых чисел окажется самой большой.
Рассмотрим пример. Один из учеников Николая Николаевича расположил в таблице числа следующим образом:
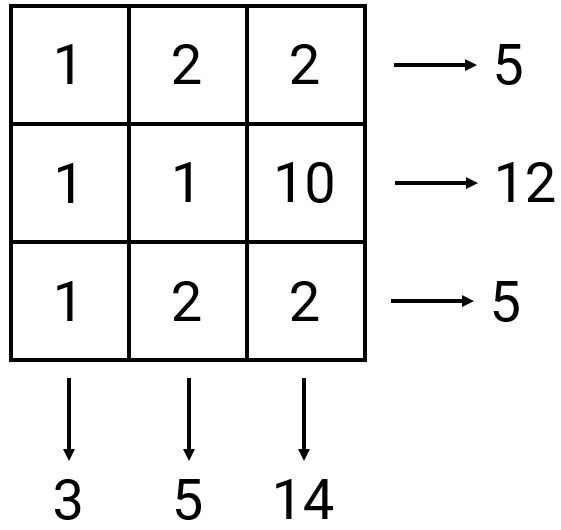
Среди полученных шести сумм по строкам и столбцам этой таблицы встречаются один раз простое число 3 и три раза простое число 5. Так как в итоге учитываются только различные простые числа, результат этого ученика равен сумме 3+5, то есть 8.
Вам предлагается поучаствовать в решении этой головоломки. Заполните ячейки в таблице целыми числами от 1 до 10. Далее проверяющая программа найдёт все суммы в вашей таблице по строкам и все суммы по столбцам и просуммирует все различные простые числа среди этих шести сумм. Чем больше окажутся значение этой суммы и количество различных простых чисел в ней, тем выше будет оценена попытка.
Замечание
Далее приводится список всех простых чисел, не превосходящих 50: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.

Ответ
Ответ:
Сначала оценим некий максимум
Максимально можно получить среди сумм из 3 чисел от 0 до 10, это 10 + 10 + 10 = 30
Минимально соответственно 0 + 0 + 0 = 0
В диапазоне от 0 до 30: – десять различных простых чисел. А надо получить 6 различных и желательно максимально возможных.
А теперь давайте поймем что каждое число в ячейке участвует в сумме 2 раза (в строке и в столбце)
Таким образом сумма строк и сумма столбцов будет равна друг другу.
А сумма всех полученных чисел будет как раз суммой все столбцов и строк.
Тогда проверим максимально возможный вариант 29 + 23 + 19 + 17 + 13 + 11 = 112
Тогда в 3 строках и в 3 столбцах должно быть по 56 и это должна быть сумма 3-х нечетных простых. Такого не получится.
Заменим тогда 11 на меньшее 7
И следующая сумма 108 – тоже не годится.
А вот следующая сумма 106 = (29 + 23 + 19 + 17 + 13 + 5) или = (29 + 23 + 19 + 17 + 11 + 7)
Пополам будет по 53 и надо разделить по 3 простых в сумме по 53
Например 29 + 19 + 5 = 53 и 23 + 17 + 13 = 53
Расставляем эти числа в суммах строк и столбцов соответсвенно и заполняем числами квадрат.
Максимальное 10 + 10 + 9 = 29 – это например 1 строка
Ну а дальше произвольно чтоб суммы получались.
Например
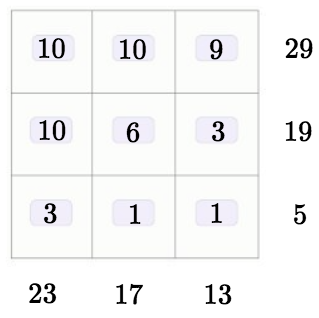
Ответ: максимум 106
