MNF =A DEF, MN = 18 см, а угол Е равен 550.
Найти длину стороны ДЕ и градусную меру угла N 2. Точка О лежит между точками P и Q, причём OP= 8 см, 0 Q = 14,5 см.
Найти расстояние между точками Р и Q. 3. Прямые АВ и СД пересекаются в точке О. Один из углов, полученных при пересечении прямых, в 5 раз меньше другого.
Найти градусные меры этих углов. 4. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса ВД.
Докажите, что ДАВД=АСВД. 5. В равнобедренном треугольнике с периметром 36 см боковая сторона относится к основанию как 4.2.
Найдите стороны треугольника.
Ответ
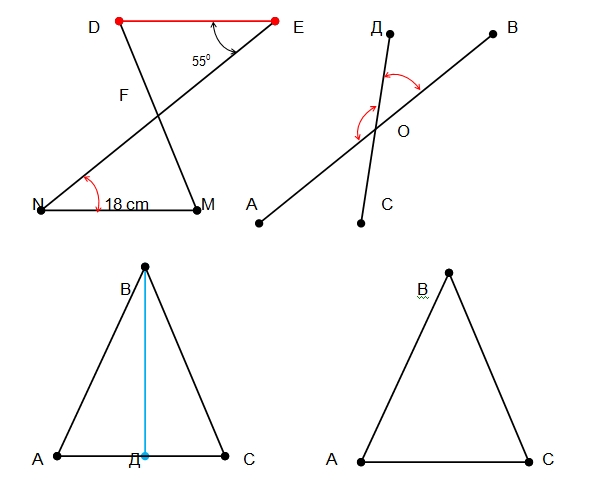
Рис. 1
Так как треугольники NBF и DEF равны, то DE = NF = 18 см, угол N = E = 55.
Ответ: DE = 18 см, угол N = 55.
2.
Так как точка О лежит между точками Р и Q, то PQ = OP + OQ = 8 + 14,5 = 22,5 см.
Ответ: 22,5 см.
3. Рис. 2
Угол АВО развернутый. Пусть угол ОВД = Х, тогда АОД = 5 * Х.
Х + 5 * Х = 180;
6 * Х = 180;
Х = ОВД = 180/6 = 30;
5 * Х = АОД = 150.
Ответ: Углы равны 30 и 150.
4. Рис. 3
Так как треугольник АВС равнобедренный, то его биссектриса ВД так же высота и медиана. Тогда АД = СД = АС / 2, треугольники АВД и СВД прямоугольные.
В прямоугольных треугольниках АВД и СВД катет ВД общий, АД = СД, тогда треугольники равны по двум катетам. Что и требовалось доказать.
5. Рис. 4
Пусть АВ = ВС = 4 * Х см, тогда АС = 2 * Х см.
Равс = 4 * Х + 4 * Х + 2 * Х = 36 см.
10 * Х = 36 см.
Х = 3,6 см.
АВ = ВС = 4 * 3,6 = 14,4 см.
АС = 2 * 3,6 = 7,2 см.
Ответ: Стороны треугольника равны 14,4 см, 14,4 см, 7,2 см.
