Ответ
Задание 1. Попарно различные числа x, y и z таковы, что xy−2z=xz−2y. Найдите x.
Задание 2. Лена сделала шарнирный подвижный четырёхугольник KLMN с длинами сторон KL=75, LM=76, MN=79 и KN=77. Какой из углов этого четырёхугольника может быть больше 180 градусов? Выберите все возможные варианты:
K
L
M
N
Ни один из перечисленных
Задание 3. На рисунке изображена фигура, состоящая из 369 единичных клеток.
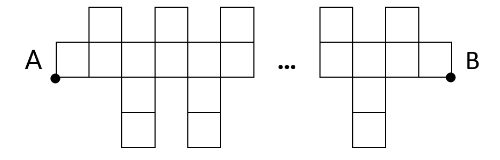
Найдите длину отрезка AB.
Задание 4. Число 328_16 делится на каждую из своих цифр. Восстановите пропущенную цифру.
Задание 5. На сторонах BC и CD квадрата ABCD отмечены точки K и L соответственно. Оказалось, что AK=2KL, ∠AKL=90, AL=10. Найдите сторону квадрата.
Задание 6. В двух кабинетах было по 30 учеников, причём в каждом из них по 15 мальчиков и 15 девочек. После того как десять учеников перебежали из второго кабинета в первый, оказалось, что 40 % учеников в первом кабинете мальчики. А сколько процентов детей во втором кабинете являются мальчиками?
Задание 7. Сто рыцарей, сто лжецов и сто болванов сидят за круглым столом в каком-то порядке. Рыцари всегда говорят правду, лжецы всегда лгут, а болваны всегда повторяют последнюю услышанную фразу. Каждый сказал одну из фраз: «Мой сосед справа рыцарь», «Мой сосед справа лжец» или «Мой сосед справа болван», причём каждую следующую фразу говорил сидящий справа от того, кто сказал предыдущую фразу. Какое наибольшее количество фраз «Мой сосед справа рыцарь» могло быть произнесено?
Задание 8. Даны a𝑎, b>0. Точки пересечения прямых y=ax+a, y=ax+b, y=bx+a и y=bx+b образуют четырёхугольник. Точка пересечения диагоналей этого четырёхугольника имеет ординату, равную 30. Найдите максимальную из ординат вершин этого четырёхугольника.
