Ответ
Задание 1. На координатной плоскости OXY отметили все точки (x , y), координаты которых удовлетворяют уравнению x2+4xy+4y2=0 . Что за множество получилось? Две параллельные прямые Одна точка Окружность Две пересекающиеся прямые Пустое множество Прямая Парабола
Задание 2. В треугольник со сторонами 6, 7 и 8 вписана окружность. Петя посчитал расстояния от каждой из вершин треугольника до ближайшей точки касания вписанной окружности со сторонами треугольника. Чему равно наименьшее из этих расстояний?
Задание 3. У Пети есть по одной карточке с цифрами 9, 7, 4, 0, 1 Он составил из них пятизначное число. Вася составил из них другое пятизначное число, вычел из большего меньшее и записал результат на доске. Получилось четырёхзначное число, состоящее из различных цифр, отличных от изначальных. Какая цифра осталась не задействована? Числа не могут начинаться с 0 .
Задание 4. Родители с сыном отправились по тропе к озеру. Сын сразу пошёл вперед, а дойдя до озера, повернул назад и шёл, пока не встретил идущих медленнее родителей. Длина его пути до озера оказалась равна 500 шагам, а назад до родителей 400 шагам. Общее потраченное сыном время до встречи с родителями т. Через сколько минут после встречи с возвращающимся сыном родители дойдут до озера? Считаем, что шаги имеют равную длину, скорости сына и родителей постоянны.
Задание 5. Натуральные корни x1 и x2 многочлена x2−bx+cтаковы, что произведение bcx1x 2 равно 11700. Найдите наибольшее возможное значение c.
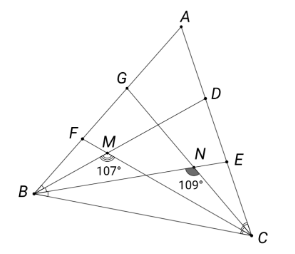
Задание 6. В треугольнике ABC отрезки BD и BE делят угол ∠ABC на три равные части. Отрезки CF и CG делят угол ∠ACB на три равные части. Отрезки BD и CF пересекаются в точке M, а отрезки BE и CG пересекаются в точке N. Известно, что ∠BMC=107∘, ∠BNC=109∘. Найдите углы треугольника ABC. ∠ABC=∠BAC
Задание 7. В кругу сидели 24 болельщика команд «Шайба» и «Зубило». Каждый болел ровно за одну из этих двух команд. Каждый болельщик сказал своему соседу слева одну из двух фраз: или «ты болеешь за ту же команду, что и мой сосед справа», или «вы с моим соседом справа болеете за разные команды». Оказалось, что ровно половина болельщиков сказала первую фразу и ровно половина вторую. При этом каждый говорил правду, если обращался к своему единомышленнику (болеющему за ту же команду), и лгал, если обращался к фанату другой команды. Какое максимальное количество болельщиков «Шайбы» могло быть?
Задание 8. В океане кораллы часто сливаются в единый организм для лучшего выживания. При слиянии двух кораллов с M и N щупальцами вместо них образуется один коралл с (M+N−1 ) щупальцами. Вначале имеется 100 кораллов с тремя щупальцами, 101 коралл с четырьмя щупальцами и 102 коралла с пятью щупальцами. После нескольких слияний остался один коралл. Какое наибольшее количество щупалец у него может быть?
