Ваня хочет построить из кубиков n пирамидок. Он собирает пирамидки следующим образом:
1. Изначально в каждой пирамидке имеется по a1 кубиков в первом ряду.
2. В каждой второй пирамидке, т.е. номер которой делится на 2, к ним добавляется по a2 кубиков во второй ряд.
3. В каждой четвёртой пирамидке, т.е. номер которой делится на 4, добавляется по a3 кубиков в третий ряд.
4. В каждой восьмой пирамидке, т.е. номер которой делится на 8, добавляется по a4 кубиков в четвёртый ряд.
И так далее.
Выразим условие более формально: в каждой пирамидке, номер которой делится на (i−1)-ую степень числа 2, к исходному числу кубиков a1 добавляется по ai кубиков в i ряд. Помогите Ване определить количество кубиков, которое ему нужно для построения всех пирамидок.
Формат входных данных
Первая строка входных данных содержит число nn (1≤n≤109) количество пирамидок, которые хочет построить Ваня.
Вторая строка входных данных содержит число kk (1≤k≤30) количество рядов, для которых известно, сколько в них будет кубиков. Гарантируется, что в каждой пирамидке не более чем k рядов.
Каждая из следующих k строк содержит aiai (1≤ai≤109) количество кубиков в i-м ряде пирамидки. Количество кубиков, требующихся для каждого следующего слоя, не убывает.
Формат выходных данных
В единственной строке выведите число количество кубиков, которые нужны Ване для постройки всех пирамидок.
Обратите внимание, что ответ в этой задаче может превышать возможное значение 32‑битной целочисленной переменной, поэтому необходимо использовать 64‑битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, тип long в Java и C#).
Система оценки
Решения, правильно работающие при n≤15, ai≤100, будут оцениваться в 20 баллов.
Решения, правильно работающие при n≤105, будут оцениваться в 50 баллов.
Замечание
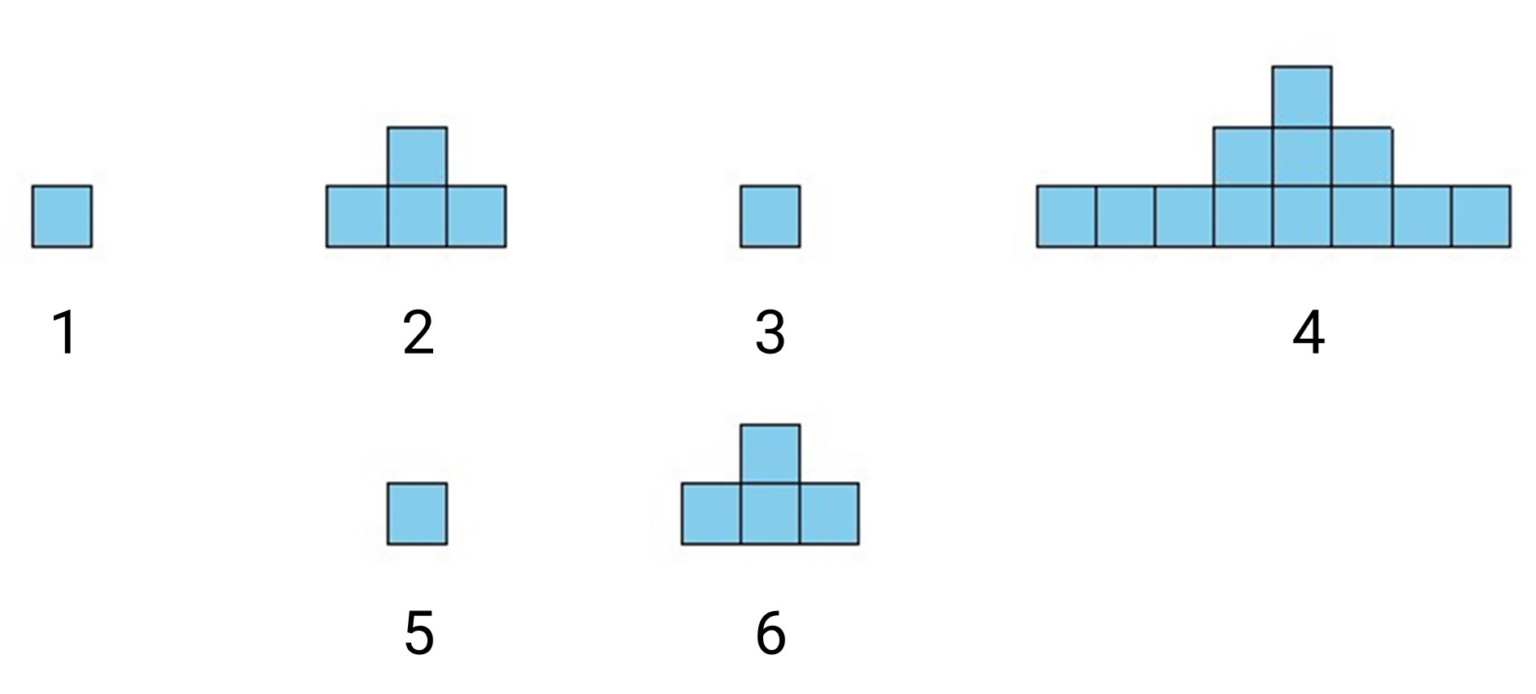
Рассмотрим первый пример. Пирамидки с нечётными номерами 1, 3, 5 имеют по одному ряду и состоят из 1 кубика. Пирамидки с номерами 2, 6 имеют по два ряда и состоят из 1+3 кубиков. Пирамидка с номером 4 имеет 3 ряда и состоит из 1+3+8 кубиков. В сумме Ване потребуется 1+(1+3)+1+(1+3+8)+1+(1+3) = 23 кубика. Пирамидки изображены на рисунке.
Ввод
6
3
1
3
8
Вывод
23
63
